1 前言
之前一直接触的是BLUP、ssGBLUP等方法,对于岭回归、贝叶斯等方法了解甚少。最近在做抗病性状的遗传评估,需要了解和评估相关算法,先从岭回归学起。
基因组选择需要解决的问题:
- 在早期,SNP标记的数量要远大于样本量,这意味着要求解的标记效应值数量远大于观察值,会存在不唯一的解。针对这个问题,提出了RRBLUP的方案。
- 但是现在问题反过来了,像奶牛分型的样本量已经达到了百万头,已经比一般的芯片,如50K要多了。现在问题是如何求解对如此庞大的样本,求解其逆矩阵。Misztal等人提出了APY算法策略,即把分型个体分为核心和非核心两类,利用少量核心个体的基因组亲缘关系逆矩阵,以及非核心与核心个体间的基因组亲缘关系矩阵,直接计算得到所有分型个体的基因组亲缘关系逆矩阵,避免了直接求逆。具体可参考ssGBLUP方法的最新综述文章:Single-Step Genomic Evaluations from Theory to Practice: Using SNP Chips and Sequence Data in BLUPF90。
本文主要想了解两个问题:
- 为什么讲RRBLUP等价于GBLUP
- RRBLUP是如何解决p>n问题的
本文主要是学习RRBLUP方法,参考了百奥云GS专栏的基因组选择之模型篇的相关叙述,感觉说的特别好。
RRBLUP vs GBLUP
RRBLUP是一种改良的最小二乘法,是间接法的代表算法。它能估计出所有SNP的效应值。该方法将标记效应假定为随机效应且服从正态分布,利用线性混合效应模型估算每个标记的效应值,然后将每个标记效应相加即得到个体的估计育种值。
GBLUP是直接法的代表,它把个体作为随机效应,根据参考群体和预测群体SNP基因型信息构建的亲缘关系矩阵作为方差协方差矩阵,通过迭代法估计方差组分,进而求解线性混合效应模型获得待预测个体的估计育种值。
2 为什么两个模型是等价的?
考虑到Endelman等RRBLUP的文章中,公式中对G的定义跟后来的基因组亲缘关系G矩阵冲突,这里综合了Hayes等文章中的定义方法。
2.1 RRBLUP模型(以标记为基础的BLUP):
\[y=ZWu+e\] 其中,\(u \sim N(0,I\sigma^{2}_{u})\),u为标记等位基因的替代效应向量;W是基因型矩阵(-1,0,1等形式);Z为观察值的关联矩阵。
假定\(K=ZW\),那么标记效应的BLUP解为: \[\hat{u}=(K'K+\lambda I)^{-1}K'y\] 其中I表示标记间是独立的,没有连锁关系。岭参数\(\lambda = \sigma^{2}_{e}/\sigma^{2}_{u}\)为残差方差与标记效应方差的比值。
上述公式可以根据经典的单性状BLUP模型公式推导: \[ \begin{bmatrix} X'X & X'K \\ K'X & K'K+\lambda I \end{bmatrix} \begin{bmatrix} \hat{b} \\ \hat{u} \end{bmatrix} = \begin{bmatrix} X'y \\ K'y \end{bmatrix} \] 由于没有模型中没有考虑固定效应,因此模型可以进一步简化为 \[ (K'K+\lambda I)\hat{u} = K'y \] 进而推导出前述公式。
2.2 常规BLUP模型
\[y=Zg+e\] 其中,\(g \sim N(0,G\sigma^{2}_{g})\),g为基因型值向量;Z为观察值的关联矩阵。
注意:RRBLUP模型中标记效应指的是每个位点某个等位基因的可替代效应;而常规BLUP模型中基因型值指的所有位点的基因型值之和,即个体水平的效应。
在系谱为基础的育种值预测过程中,G指的是根据共亲系数计算得到的加性亲缘关系矩阵A。
从2个模型中可以看出\(g=Wu\),基因型值即个体育种值的遗传方差:
\[V(g)=G\sigma^{2}_{g}=V(Wu)=WW'\sigma^{2}_{u}\] 如上所述,这两个模型是等同的。
因此,G矩阵也可以根据W矩阵计算得到:
\(G = WW'\sigma^{2}_{u}/\sigma^{2}_{g}\)。此时,G为基因组亲缘关系矩阵。
因此,\(G\)的另外一个特性:基于该矩阵计算得到的GEBV等同于利用RRBLUP模型计算得到的结果。
3 岭回归分析的原理
现在来看第二个问题:为什么岭回归可以解决p>n的问题。
岭回归类似于Bayesian A,假定每个SNP的效应值的相等的,符合正态分布。
当标记数量远超过观测值时,譬如有500个体的体重观测值,需要估计5万个SNP标记的效应,如果没有惩罚措施,用最小二乘估计方法,会导致预测值标准误较大,且最小二乘回归估计值\(\beta\)不唯一。
回归系数的计算公式为: \[ \beta=(K'K)^{-1}K'y \] 其中K为设计矩阵(为了跟第一部分呼应)。可以看出,\(\beta\)估计值依赖K。如果K为病态矩阵,那么K’K非常有可能是是奇异的或者接近奇异,直接会导致没有逆矩阵,因此会无解。
奇异(singular)的定义:该矩阵的行列式值为0。奇异表示矩阵中列存在依赖关系,并不独立。奇异只能是对应方阵而言的。为什么当一个矩阵的行列式(determinant)为0时,称矩阵为奇异,这里有一个比较容易理解的解释,大意是这样:
…为何只说行列式为零的矩阵才奇异呢?这很可能是由线性方程组的解的个数引出的名词。对于系数行列式非零的情况,方程组的解是唯一的;否则,就有无穷多解。换句话说,系数行列式可能取各种值,但不管是什么值,只要不为零,相应的方程组的解一定是唯一的。但是,如果系数行列式恰巧为零,方程组的解就可以有无穷多。这样,行列式为零的矩阵就显得很“突出”、很“不一样”、很“另类”、很“奇怪”,等等。而“奇异”包含了奇怪和异端两种意思,正好用于描述这种矩阵。奇异矩阵对应的英文单词是“singular matrix”,其中“singular”有如下几种意思(参见《朗文英语辞典》):1. a singular noun, verb, form etc is used when writing or speaking about one person or thing; 2. very great or very noticeable; 3. very unusual or strange. 显然,“singular matrix”中的“singular”对应上面的第3个意思,也带有第2个意思。
普通最小二乘估计的的核心思想是,让残差平方和(sum of squared residuals, RSS)最小:
\[ RSS =\sum^{n}_{i=1}(y_{i}-\hat{y_{i}})^{2} \] 其中\(y_{i}\)和\(\hat{y_{i}}\)分别为观测值和模型预测值,n为观测值个数。
岭回归的方法,如前所述,加入一个惩罚项\(\lambda\),让修改后的\(RSS_{ridge}\)最小 \[ RSS_{ridge} =\sum^{n}_{i=1}(y_{i}-\hat{y_{i}})^{2}+\lambda \sum^{p}_{j=1}\beta_{j}^{2} \] \(\lambda\)的选择是非常重要的,太小,不起作用,等同于普通最小二乘估计值;太大,回归系数估计值趋向于0,对模型的解释能力变弱。
因此在使用岭回归的过程中,需要保持方差和偏差之间的一个平衡。
\[MSE = Variance + Bias^{2} + Irreducible error\] 公式的解释,见这里。MSE,指的是mean squared error,即平均平方误差。
选择一个\(\lambda\)值,方差MSE持续降低,偏差增加很少,Test MSE最小,如下图所示。

方差与偏差的平衡
4 基于R的实例解析
参考这个链接。
4.1 数据集
使用的数据集为集成在R中的mtcars,它来自datasets包。该数据集是Motor Trend US 杂志收集的1973到1974年期间总共32辆汽车的11个指标: 油耗及10个与设计及性能方面的指标。
print(mtcars)## mpg cyl disp hp drat wt qsec vs am gear carb
## Mazda RX4 21.0 6 160.0 110 3.90 2.620 16.46 0 1 4 4
## Mazda RX4 Wag 21.0 6 160.0 110 3.90 2.875 17.02 0 1 4 4
## Datsun 710 22.8 4 108.0 93 3.85 2.320 18.61 1 1 4 1
## Hornet 4 Drive 21.4 6 258.0 110 3.08 3.215 19.44 1 0 3 1
## Hornet Sportabout 18.7 8 360.0 175 3.15 3.440 17.02 0 0 3 2
## Valiant 18.1 6 225.0 105 2.76 3.460 20.22 1 0 3 1
## Duster 360 14.3 8 360.0 245 3.21 3.570 15.84 0 0 3 4
## Merc 240D 24.4 4 146.7 62 3.69 3.190 20.00 1 0 4 2
## Merc 230 22.8 4 140.8 95 3.92 3.150 22.90 1 0 4 2
## Merc 280 19.2 6 167.6 123 3.92 3.440 18.30 1 0 4 4
## Merc 280C 17.8 6 167.6 123 3.92 3.440 18.90 1 0 4 4
## Merc 450SE 16.4 8 275.8 180 3.07 4.070 17.40 0 0 3 3
## Merc 450SL 17.3 8 275.8 180 3.07 3.730 17.60 0 0 3 3
## Merc 450SLC 15.2 8 275.8 180 3.07 3.780 18.00 0 0 3 3
## Cadillac Fleetwood 10.4 8 472.0 205 2.93 5.250 17.98 0 0 3 4
## Lincoln Continental 10.4 8 460.0 215 3.00 5.424 17.82 0 0 3 4
## Chrysler Imperial 14.7 8 440.0 230 3.23 5.345 17.42 0 0 3 4
## Fiat 128 32.4 4 78.7 66 4.08 2.200 19.47 1 1 4 1
## Honda Civic 30.4 4 75.7 52 4.93 1.615 18.52 1 1 4 2
## Toyota Corolla 33.9 4 71.1 65 4.22 1.835 19.90 1 1 4 1
## Toyota Corona 21.5 4 120.1 97 3.70 2.465 20.01 1 0 3 1
## Dodge Challenger 15.5 8 318.0 150 2.76 3.520 16.87 0 0 3 2
## AMC Javelin 15.2 8 304.0 150 3.15 3.435 17.30 0 0 3 2
## Camaro Z28 13.3 8 350.0 245 3.73 3.840 15.41 0 0 3 4
## Pontiac Firebird 19.2 8 400.0 175 3.08 3.845 17.05 0 0 3 2
## Fiat X1-9 27.3 4 79.0 66 4.08 1.935 18.90 1 1 4 1
## Porsche 914-2 26.0 4 120.3 91 4.43 2.140 16.70 0 1 5 2
## Lotus Europa 30.4 4 95.1 113 3.77 1.513 16.90 1 1 5 2
## Ford Pantera L 15.8 8 351.0 264 4.22 3.170 14.50 0 1 5 4
## Ferrari Dino 19.7 6 145.0 175 3.62 2.770 15.50 0 1 5 6
## Maserati Bora 15.0 8 301.0 335 3.54 3.570 14.60 0 1 5 8
## Volvo 142E 21.4 4 121.0 109 4.11 2.780 18.60 1 1 4 2选择hp(总功率)作为因变量,mpg(油耗)、wt(重量)、drat(后轴比)、qsec(提速能力1/4英里需要的时间)作为自变量。
利用glmnet包来进行岭回归分析。
Glmnet is a package that fits generalized linear and similar models via penalized maximum likelihood. The regularization path is computed for the lasso or elastic net penalty at a grid of values (on the log scale) for the regularization parameter lambda. The algorithm is extremely fast, and can exploit sparsity in the input matrix x.
该包要求因变量为向量,自变量为datamatrix格式。
library(glmnet)## 载入需要的程辑包:Matrix## Loaded glmnet 4.1-1y = mtcars$hp
x <- data.matrix(mtcars[,c("mpg","wt","drat","qsec")])4.2 拟合岭回归模型
使用glmnet()函数拟合岭回归模型。需要注意,alpha值设置为0。
不同alpha值对应的处理方法:
- 0 岭回归 Ridge regression
- 1 拉索回归 Lasso regression
- 0-1 弹性网络 Elastic net
此外,岭回归需要对数据进行归一化处理,即平均值为0,方差为1。glmnet包会自动进行标准化处理。
ridge_reg_model <- glmnet(x, y, alpha = 0)
summary(ridge_reg_model)## Length Class Mode
## a0 100 -none- numeric
## beta 400 dgCMatrix S4
## df 100 -none- numeric
## dim 2 -none- numeric
## lambda 100 -none- numeric
## dev.ratio 100 -none- numeric
## nulldev 1 -none- numeric
## npasses 1 -none- numeric
## jerr 1 -none- numeric
## offset 1 -none- logical
## call 4 -none- call
## nobs 1 -none- numeric4.3 选择优化的\(\lambda\)值
通过K折交叉验证方法,计算test MSE。汇总不同\(\lambda\)值对应的test MSE,选择最小test MSE对应的\(\lambda\)值。
cv.glmnet()函数可以执行多折交叉验证,如5折或者10折等。本文执行10折交叉验证
cv_model <- cv.glmnet(x, y, alpha = 0, nfolds = 10)
best_lambda_s <- cv_model$lambda.min画出\(\lambda\)值对应的test MSE,如下图所示。最优\(\lambda\)值对应图中x轴的log(best_lambda_s)=2.4932095位置。
plot(cv_model)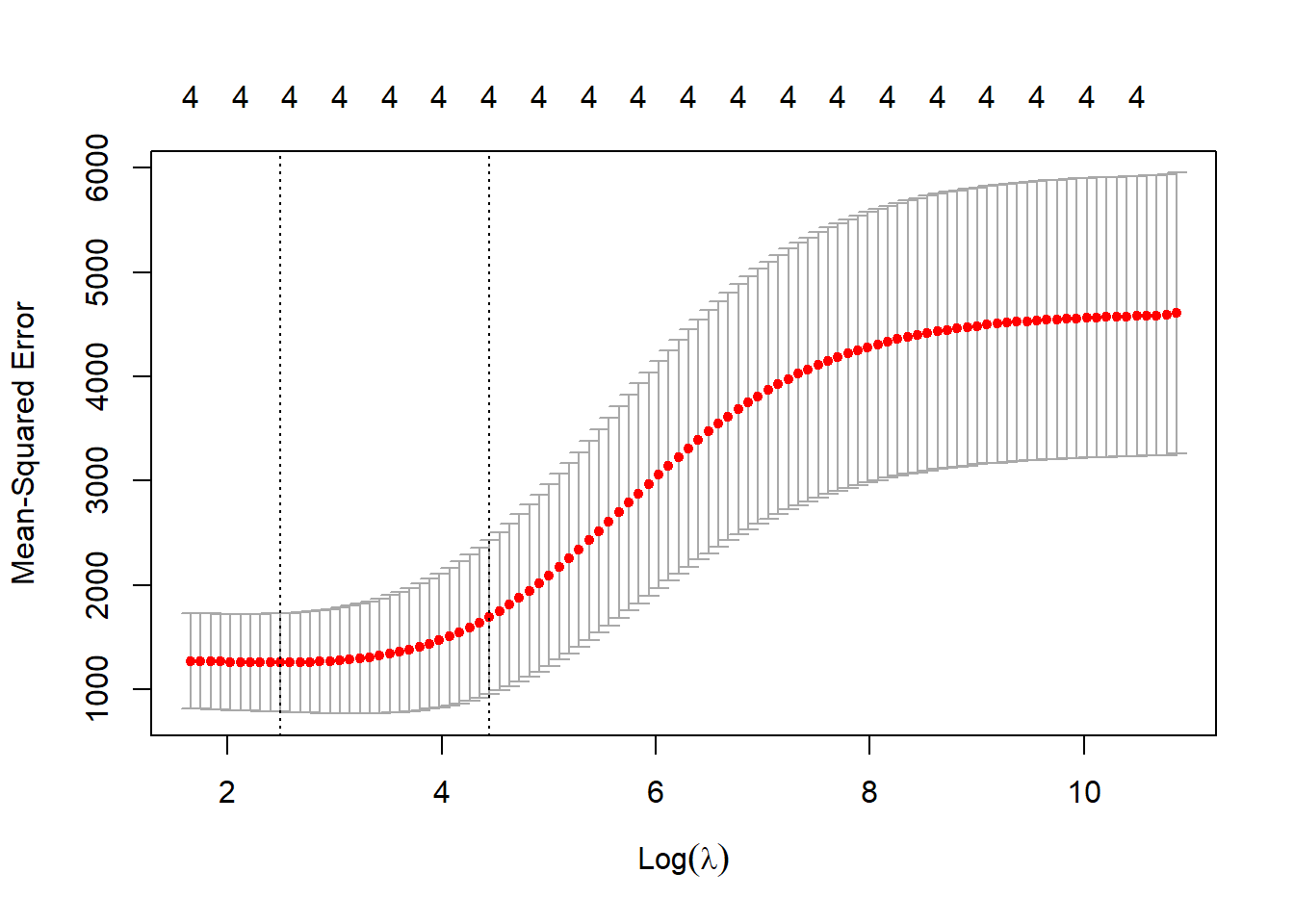
Figure 1: lambda值与test MSE的对应关系图
4.4 拟合最优模型
根据确定的\(\lambda\)值,重新拟合模型。
best_model <- glmnet(x, y, alpha = 0, lambda = best_lambda_s)
coef(best_model)## 5 x 1 sparse Matrix of class "dgCMatrix"
## s0
## (Intercept) 472.444103
## mpg -3.290491
## wt 18.817693
## drat -2.038402
## qsec -17.528318根据计算出来的回归系数,建立对总功率hp的预测模型:
hp = 472.4441033 + -3.2904912mpg + 18.8176927wt + -2.038402drat + -17.5283176qsec
这样就可以根据这四个指标预测不同类型摩托的总功率了。
画一个回归系数随着\(\lambda\)值变化的轨迹图,可以看到,随着\(\lambda\)值的不断变大,最终所有的回归系数归零。这就是为什么叫岭(脊)回归的原因?!
library(latex2exp)
plot(ridge_reg_model, xvar = "lambda", xlab=TeX('$Log(\\lambda)'))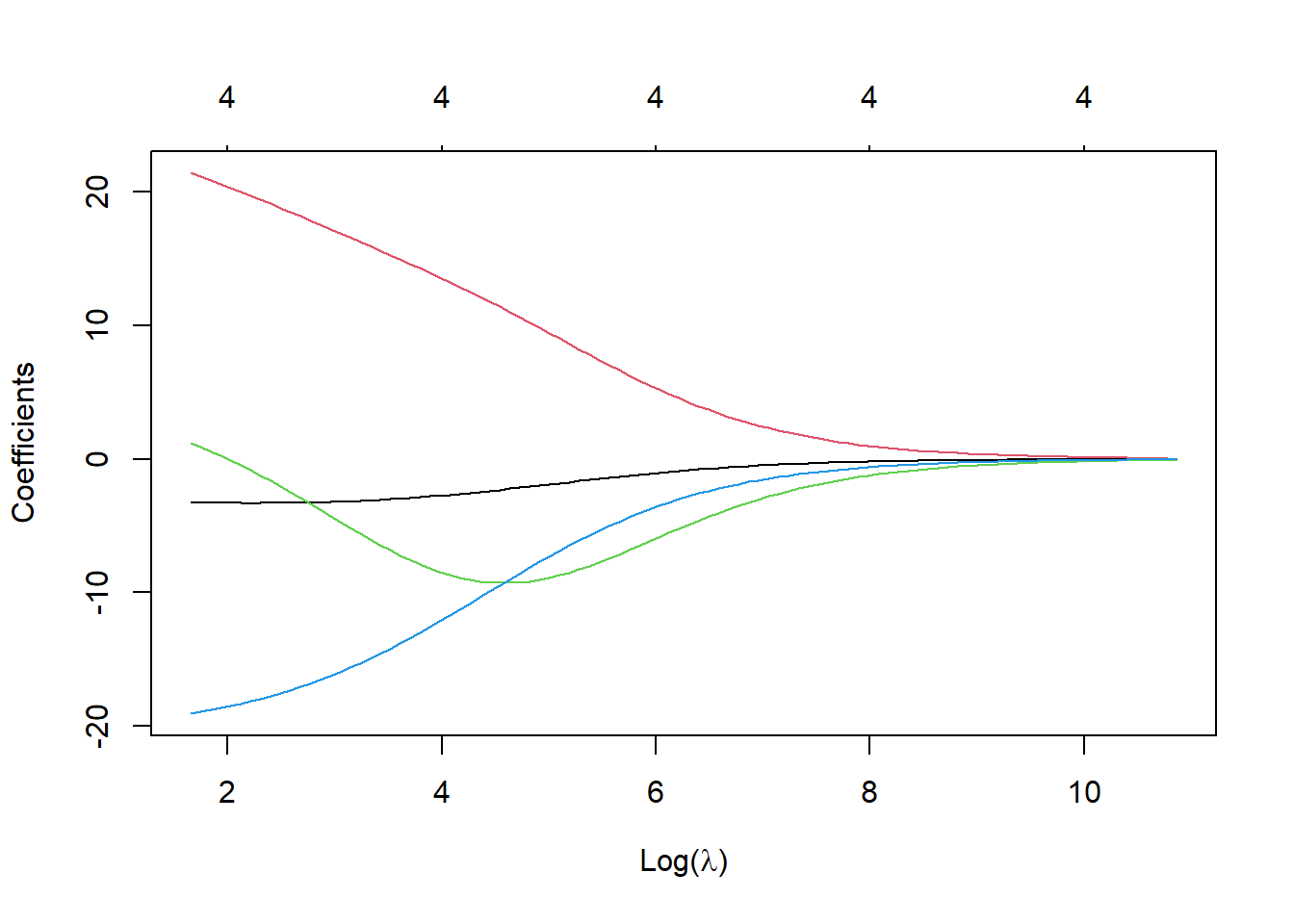
Figure 2: \(\lambda\)值与回归系数的对应关系
还剩下一个问题,为什么在RR-BLUP算法中,直接设定\(\lambda = \sigma^{2}_{e}/\sigma^{2}_{u}\),即残差方差与标记效应方差的比值? 这个问题,一直没有找到答案,感觉由于是跟BLUP模型等同,所以才推导出这样的结果。
其实可以这样了解?:REML方法,通过迭代估计残差方差和加性遗传方差,也就是在不断寻找最优\(\lambda\)的过程?这需要看一下REML算法的过程了。