首先加载本篇blog用到的5个包。data.table用于处理数据;ggplot2画图;ISLR包来自《An Introduction to Statistical Learning with Applications in R 》这本书,这个包提供了书中用到的数据,本文使用了一个关于信用卡违约的模拟数据集Default;VGAM包和MASS分别提供vglm()和polr()函数对多分类变量进行分析。这些包均可从cran上直接下载和安装。
knitr::opts_chunk$set(fig.align = "center")
library(data.table)
library(ggplot2)
library(ISLR)
library(VGAM)
library(MASS)Logit和probit连接函数,是在利用广义线性模型(GLMM),主要是阈值模型处理二分变量或者分类变量时,经常用到的两个函数。但对于为什么要使用它们的原因并不是很清楚。本文试着把近期看到的一些材料理解并记录下来。
本文参考了以下材料:
- Fox John, 2010. Logit and Probit Models notes.
- 王济川, 郭志刚, 2001. Logistic回归模型——方法与应用全书.
- James G, et al, 2017. An Introduction to Statistical Learning with Applications in R.
- Lesson 8: Multinomial Logistic Regression Models。有实际可运行的R例子,建议关注。
1. 当因变量为分类变量时,为什么要引入Logistic分布函数处理模型?
如果反应变量即因变量(response or dependent variable) 属于连续变量(continuous variable)类型,通常用线性混合模型处理。譬如社会科学中关于个人收入相关的模型;自然科学中动物收获体重的相关模型等。
然而当因变量为分类变量(categorical variable)类型时,如社会科学中个人信用卡还款是否违约;自然科学中一尾虾的存活状态等,利用线性模型就不合适了。
为了处理分类性状,统计学家引入了哑变量或虚拟变量的概念(Dummy variable),对不同的类别用数字表示。譬如一尾虾的存活状态,存活=1,死亡=0等。
下边,利用ISLR包中的信用卡还款违约数据集Default来作为例子说明,为什么线性模型不适合处理分类数据。数据集的探索性分析见散点和箱线图。
Default_dt <- as.data.table(Default)
Default_dt## default student balance income
## 1: No No 729.5265 44361.63
## 2: No Yes 817.1804 12106.13
## 3: No No 1073.5492 31767.14
## 4: No No 529.2506 35704.49
## 5: No No 785.6559 38463.50
## ---
## 9996: No No 711.5550 52992.38
## 9997: No No 757.9629 19660.72
## 9998: No No 845.4120 58636.16
## 9999: No No 1569.0091 36669.11
## 10000: No Yes 200.9222 16862.95ggplot(data = Default_dt, aes(x = balance,
y = income,
color = default,
shape = default)) +
geom_point(alpha = 0.3) +
labs(x="信用卡欠款(balance)", y="收入(income)") 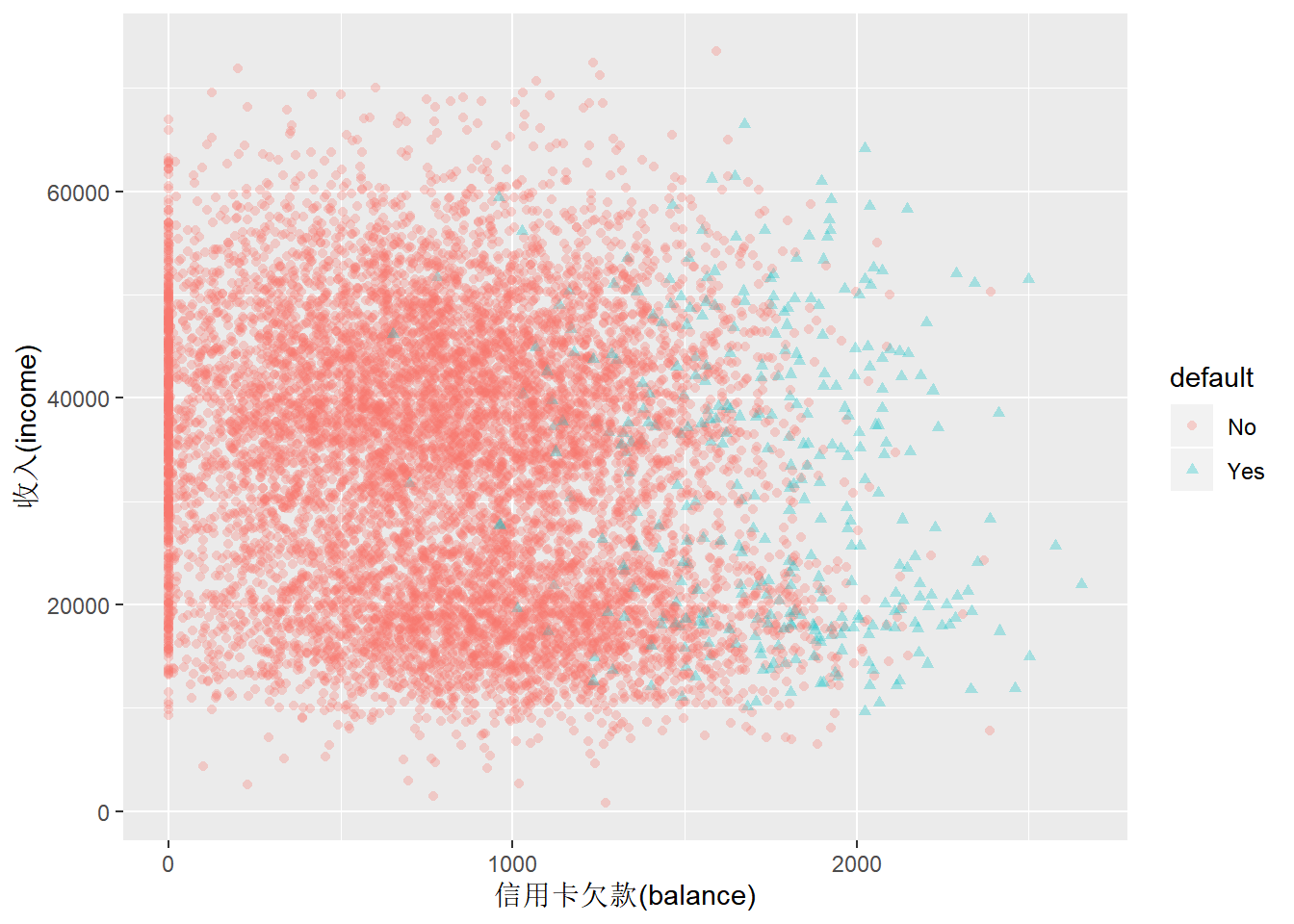
Figure 1: 个人收入与信用卡欠款散点图
从图1散点图中可以看出,个人收入跟信用卡还款是否违约没有关系,但是跟信用卡欠款额有很大关系。图2箱线图进一步验证了这个趋势。
ggplot(data = Default_dt, aes(x = default,
y = balance,
color = default)) +
geom_boxplot() +
labs(x="违约(default)", y="信用卡欠款(balance)") 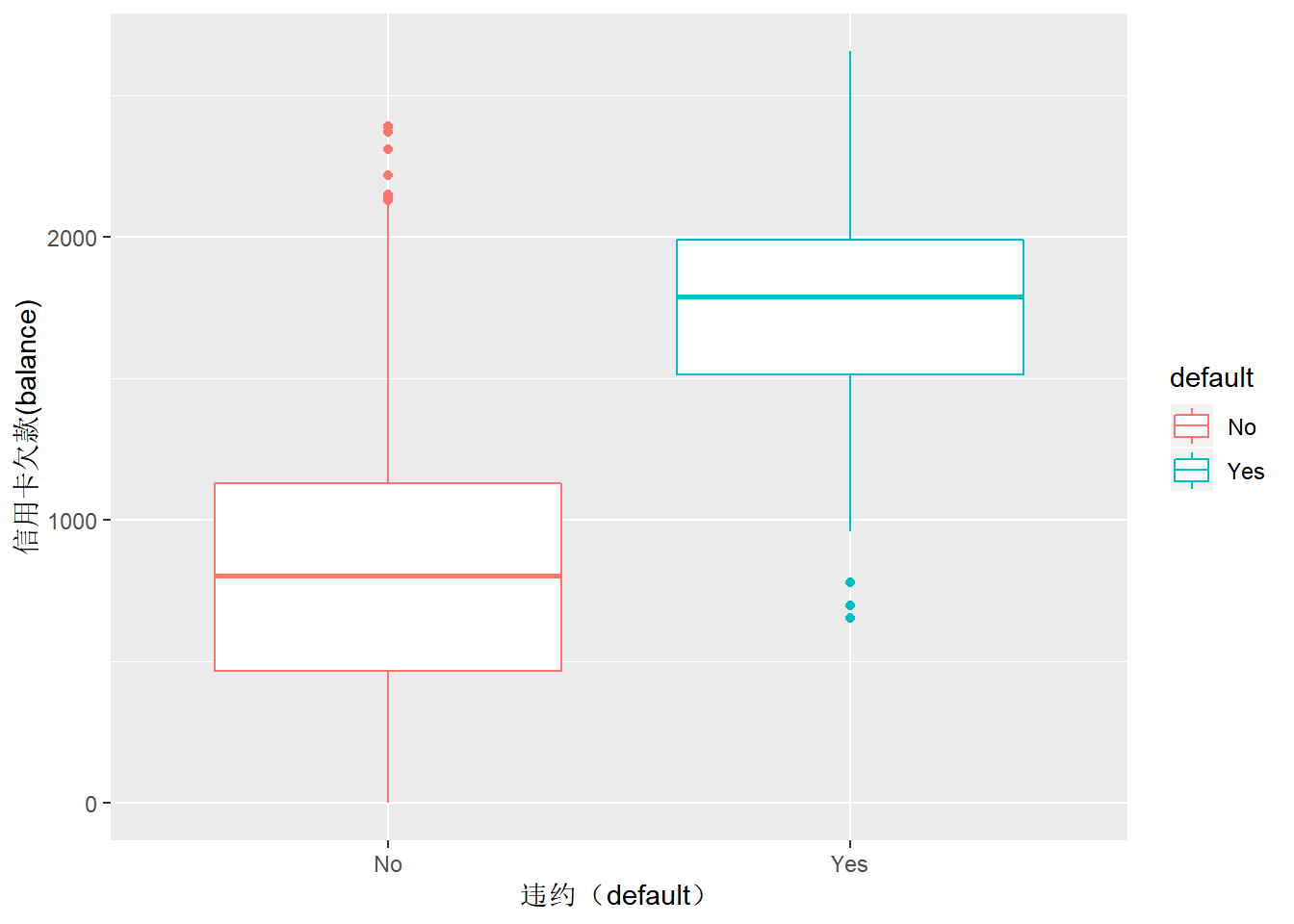
Figure 2: 信用卡是否违约用户欠款箱线图
针对信用卡还款是否违约,建立一个线性模型: \[y_{i}=\alpha+\beta x_{i}+\varepsilon_{i}\]
\(y_{i}\)是一个二分变量,表示第i个样本的信用卡还款状态,违约=1,不违约=0;如果分析的是信用卡不违约的发生率,那么违约=0,不违约=1;\(\varepsilon_{i}\)为独立残差,\(\varepsilon_{i}\)~\(N(0,\sigma^{2}_{\varepsilon})\) 。如果x是随机的,应该与\(\varepsilon\)的关系是独立。
\(y_{i}\)的期望可以表述为:
\[E(y_{i}|x_{i})=E(\alpha+\beta x_{i}+\varepsilon_{i})=\alpha+\beta x_{i}\]
因为\(y_{i}\)是二分变量,取值只能为0或者1。因此,\(y_{i}\)的期望实:\(E(y_{i}|x_{i})=P(y_{i}=1|x_{i})\),可以解释为第i个人信用卡违约的概率。因此可以把方程的左侧作为事件发生的概率来解释。因变量为二分类型的线性模型也被称为线性概率模型(Linear Probability Model, LPM)。
LPM模型在处理二分变量(binary or dichotomous variable)时,存在以下缺陷:
- 非正态性。因为因变量为二分变量,因此残差也是二分变量,不符合正态性。然而,参考中心极限定理,正态性的假定条件对于利用最小二乘法进行参数估计的正态概率模型,并不是特别关键的限制因素。
- 残差并不固定。\(Var(\varepsilon_{i})=P(y_{i}=1|x_{i})×P(y_{i}=0|x_{i})\)。从这个公式中,可以看到残差方差受自变量x的影响,不同的自变量有不同的方差,产生方差的非齐性,违反了x与残差互相独立的原则。
- 因变量(二分变量)与自变量之间,截距和斜率并不是固定的,在不同的区间,有不同的值。当\(x_{i} <= -\frac{\alpha}{\beta}\)时,截距和斜率都为0;当\(-\frac{\alpha}{\beta} <= x_{i} <= \frac{(1-\alpha)}{\beta}\)时,截距为\(\alpha\),斜率为\(\beta\);当\(x_{i} >=\frac{(1-\alpha)}{\beta}\)时,截距为1,斜率为0。LPM模型无法拟合这种非线性关系,会出现概率小于0或者大于1的情况。
如果基于信用卡欠款变量balance,建立线性回归模型,预测一个人是否会违约,由于因变量只有0和1两种状态,当balance非常小时,预测值将会出现负值(图3),预测不准确。
Default_dt[default %in% c("No"), default_num:=0]
Default_dt[default %in% c("Yes"), default_num:=1]
default_lm1 <- lm(default_num ~ balance, data=Default_dt)
summary(default_lm1)##
## Call:
## lm(formula = default_num ~ balance, data = Default_dt)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.23533 -0.06939 -0.02628 0.02004 0.99046
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -7.519e-02 3.354e-03 -22.42 <2e-16 ***
## balance 1.299e-04 3.475e-06 37.37 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.1681 on 9998 degrees of freedom
## Multiple R-squared: 0.1226, Adjusted R-squared: 0.1225
## F-statistic: 1397 on 1 and 9998 DF, p-value: < 2.2e-16default_fitted_dt <- data.table(x=Default_dt$balance, y=default_lm1$fitted.values)
ggplot(default_fitted_dt,aes(x,y)) + geom_point() +
geom_hline(yintercept = 0) + geom_hline(yintercept = 1) +
labs(y="违约概率(default)", x="信用卡欠款额(balance)") 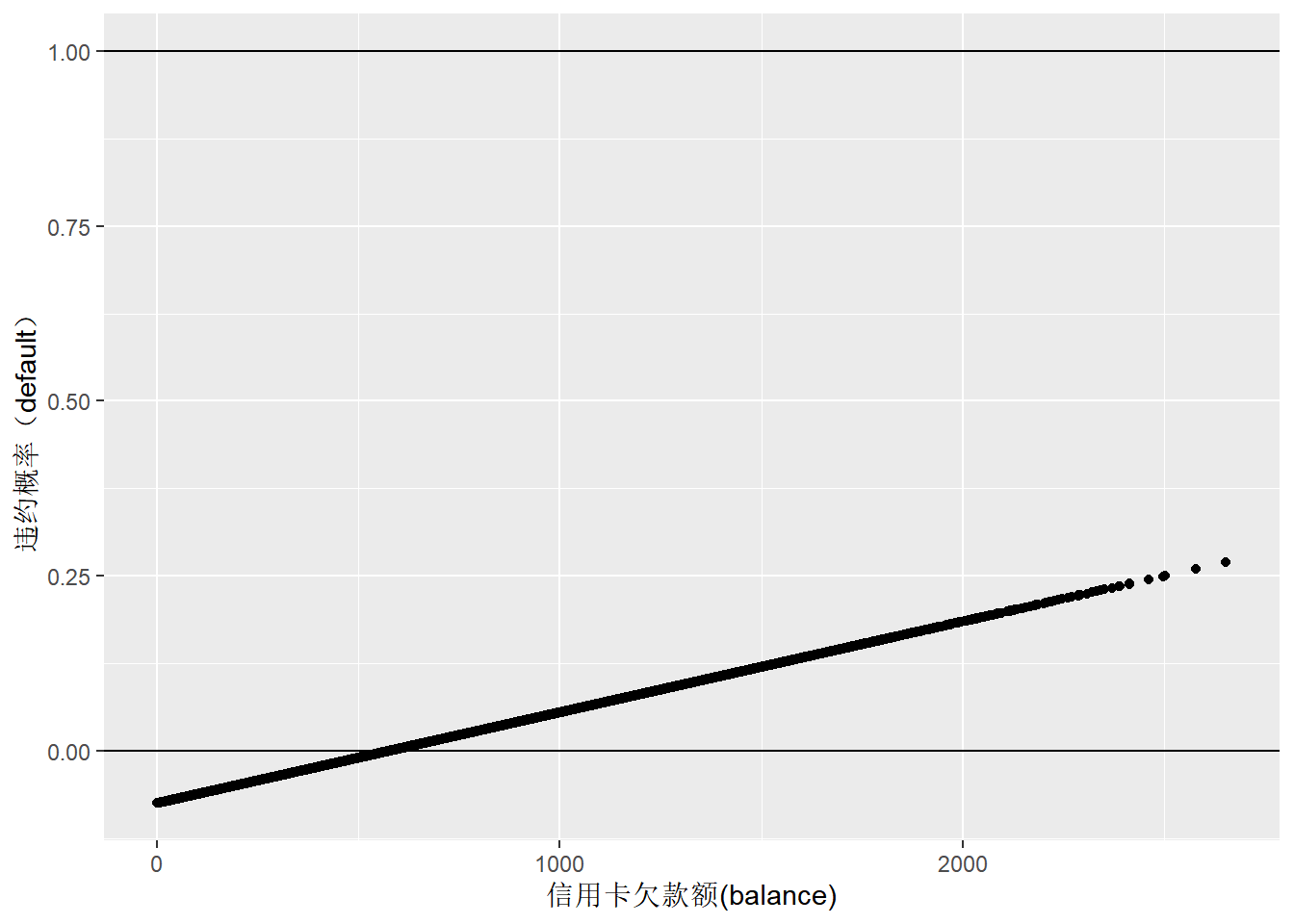
Figure 3: 信用卡欠款额与违约概率的线性回归预测
2. 转换函数
针对上述问题,当前的思路是寻找合适的转换函数,将模型输出为不同分类事件发生的概率。
2.1 将模型输出转换为概率的合理性证明
假设存在一个连续反应变量\(y_{i}^{*}\),代表事件发生的可能性,当\(y_{i}^{*}>0\)时,事件发生(\(y_{i}=1\)),反之则不发生(\(y_{i}=0\))。用下述公式表示: \[ y_{i} = \left\{\begin{matrix} 1 & y_{i}^{*} >0 \\ 0 & y_{i}^{*} \leqslant0 \end{matrix}\right. \] 假设\(y_{i}^{*}\)与\(x_{i}\)之间存在一种线性关系: \[y_{i}^{*} = \alpha+\beta x_{i}+\varepsilon_{i}\] 可以推导出,事件发生的概率: \[ P(y_{i}=1|x_{i}) \\ = P(y_{i}^{*}>0) \\ = P((\alpha+\beta x_{i}+\varepsilon_{i})>0) \\ = P(\varepsilon_{i}>(-\alpha-\beta x_{i})) \]
假设残差项\(\varepsilon_{i}\)符合逻辑斯蒂logistic分布或者标准正态分布时,根据对称性,上述公式可以做如下转换,推导出累积分布函数形式: \[ P(y_{i}=1|x_{i}) \\ = P(\varepsilon_{i}>(-\alpha-\beta x_{i})) \\ = P(\varepsilon_{i}\leqslant(\alpha+\beta x_{i})) \\ = F(\alpha+\beta x_{i}) \] 分布函数表示残差变量\(\varepsilon_{i}\)在区间\((-\infty,\alpha+\beta x_{i})\)上的概率。上述公式实际上是证明了,利用概率累积分布函数来转换数据的合法性。
接下来看转换的基本原则(这三个原则特别重要):
- 需要找到针对\(P(x)\)的函数,确保对任意\(x\)值,输出范围在0-1之间。
- 满足\(P(\alpha+\beta x_{i})\)要求的概率累积分布函数(cumulative distribution function, CDF)优先考虑。
- 转换函数需要是平滑和对称的,渐近线(asymptotes)分别为0和1。
2.2 Logit转换
logistic累积分布函数(CDF)形式为: \[ P(y_{i}=1|x_{i}) \\ = P(\varepsilon_{i}\leqslant(\alpha+\beta x_{i})) \\ = F(\alpha+\beta x_{i}) \\ = \frac{e^{\alpha+\beta x_{i}}}{1+e^{\alpha+\beta x_{i}}} \\ = \frac{1}{1+e^{-(\alpha+\beta x_{i})}} \\ = \frac{1}{1+e^{-\varepsilon_{i}}} \] 依据logistic累积分布函数计算得到的概率如图4所示,为s曲线,在0和1之间。满足前边提到的第1条原则。
x <- seq(-5,5,0.01)
y <- 1/(1+exp(-x))
logistic_dt <- data.table(x,y)
ggplot(data = logistic_dt, aes(x,y)) +geom_point()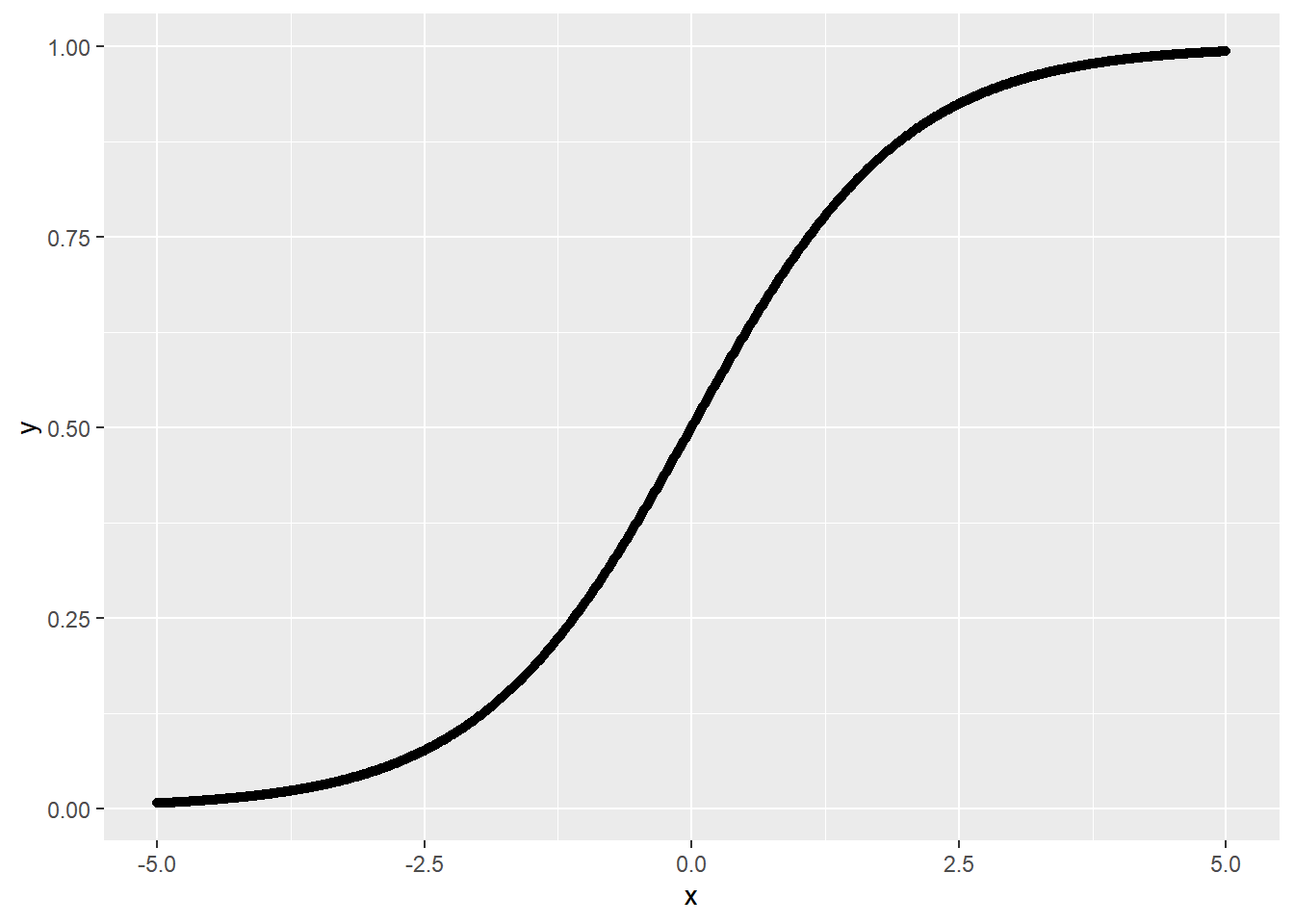
Figure 4: logistic分布函数的曲线图
ps:在机器学习中,logistic函数也被称为sigmoid函数,在神经网络中,作为激活函数。
标准logistic分布的概率密度函数(probility density function, PDF)的一般形式为: \[f(x)=\frac{e^{x}}{(1+e^{x})^2}\]
x <- seq(-5,5,0.01)
y <- exp(x)/((1+exp(x))^2)
logistic_PDF_dt <- data.table(x,y)
ggplot(data = logistic_PDF_dt, aes(x,y)) +geom_point()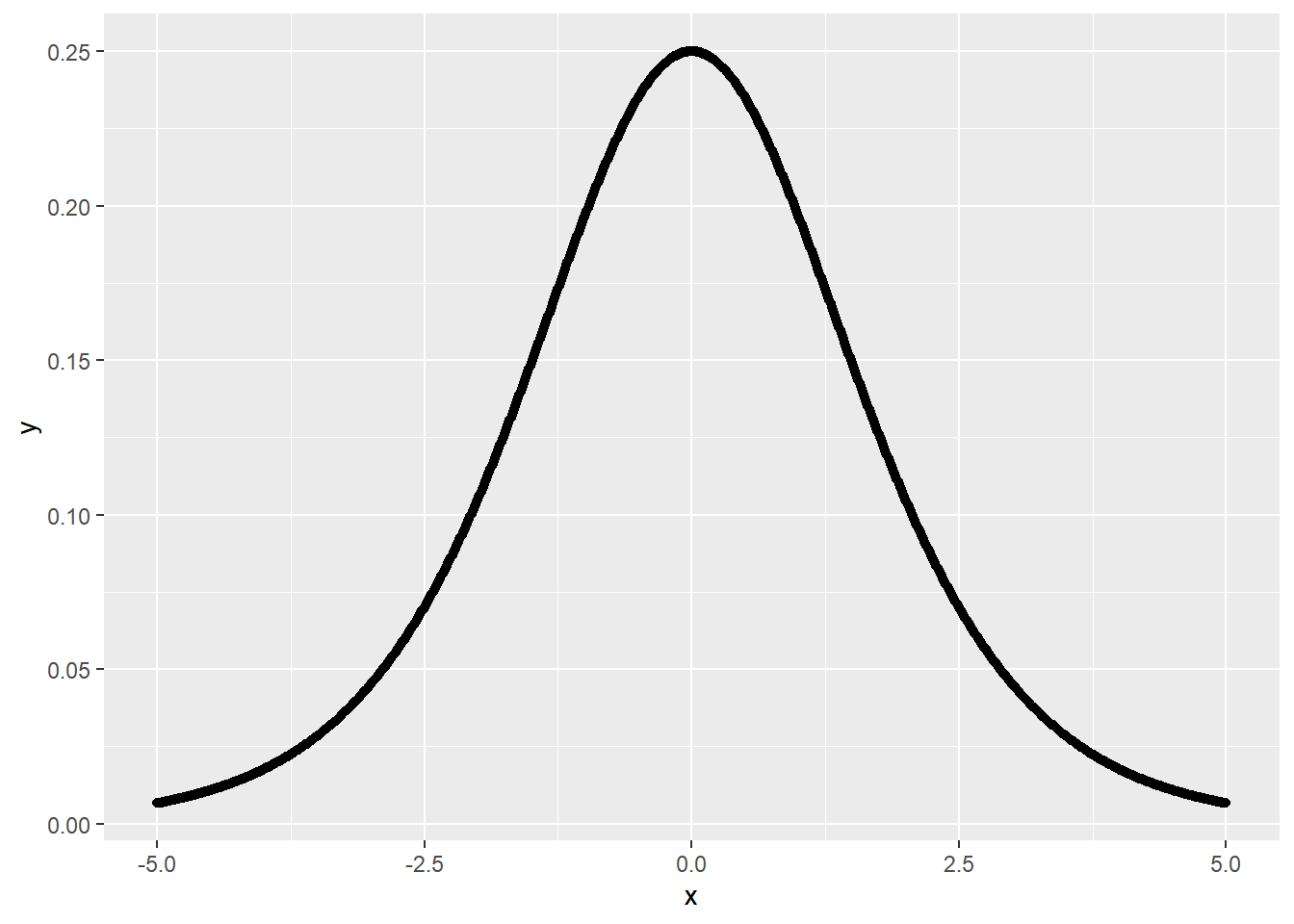
Figure 5: logistic分布概率密度曲线
概率密度函数是在计算连续变量的累积分布函数时导入的一个概念,根据概率密度函数进行积分运算,可以得到事件发生的概率。 \[F(x) = \int_{-\infty}^{\alpha}\frac{e^{x}}{(1+e^{x})^2}dx \\ = \frac{e^{\alpha}}{1+e^{\alpha}} \] 因为\(\alpha\)可以是任何数,因此可以用x替换\(\alpha\),上述公式可以变为更加普通形式: \[F(x)=\frac{e^{x}}{1+e^{x}}\]
标准logistic分布的平均值为0,方差为\(\pi^2/3=3.29\)。具体的推导过程见这里。
进一步整理思路,用\(p_{i}\)表示事件发生的概率。
\[p_{i}=\frac{e^{\alpha+\beta x_{i}}}{1+e^{\alpha+\beta x_{i}}}=\frac{1}{1+e^{-(\alpha+\beta x_{i})}}\]
针对上述公式,求解\(\alpha\)和\(\beta\)等参数非常关键。在实际计算过程中,是通过极大似然法等迭代计算的。譬如某些样本违约1,某些样本没有违约0,那么利用logistic分布函数,通过极大似然等方法,不断的迭代带入新的\(\alpha\)和\(\beta\)参数,使所有违约人的\(p\)接近1,未违约人的\(p\)值接近0。
评论:原来以为是直接把0,1数据进行转换,实际上是用logistic分布函数,通过似然法估计模型右手边参数,最后通过分布函数输出的就是概率值,自然在0-1之间了。
进一步推导上述公式: \[ p_{i}(1+e^{\alpha+\beta x_{i}})=e^{\alpha+\beta x_{i}}\\ p_{i}(1+e^{\alpha+\beta x_{i}})-e^{\alpha+\beta x_{i}}=0\\ p_{i}=e^{\alpha+\beta x_{i}}-p_{i}e^{\alpha+\beta x_{i}}\\ p_{i}=e^{\alpha+\beta x_{i}}(1-p_{i})\\ \frac{p_{i}}{1-p_{i}}=e^{\alpha+\beta x_{i}}\\ ln(\frac{p_{i}}{1-p_{i}})=\alpha+\beta x_{i}\\ \]
上述公式左手边通常表示事件发生比(Odd)的自然对数,右边是模型。上边的公式,实际上是把连接函数推导出来了。它表示把事件发生比的自然对数与模型连接在一起。
通常logit指的是\(ln(\frac{p_{i}}{1-p_{i}})\)。
利用logit连接函数,通过glm()函数重新分析信用卡违约数据。可以看到,新建立的模型可以很好地预测违约概率。没有再出现违约概率为负值的情况(图5)。
default_glm1 <- glm(default_num ~ balance, family = binomial(link = "logit"), data=Default_dt)
summary(default_glm1)##
## Call:
## glm(formula = default_num ~ balance, family = binomial(link = "logit"),
## data = Default_dt)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.2697 -0.1465 -0.0589 -0.0221 3.7589
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -1.065e+01 3.612e-01 -29.49 <2e-16 ***
## balance 5.499e-03 2.204e-04 24.95 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 2920.6 on 9999 degrees of freedom
## Residual deviance: 1596.5 on 9998 degrees of freedom
## AIC: 1600.5
##
## Number of Fisher Scoring iterations: 8default_fitted_dt <- data.table(x=Default_dt$balance, y=default_glm1$fitted.values)
ggplot(default_fitted_dt,aes(x,y)) + geom_point() +
geom_hline(yintercept = 0) + geom_hline(yintercept = 1) +
labs(y="违约概率(default)", x="信用卡欠款额(balance)") 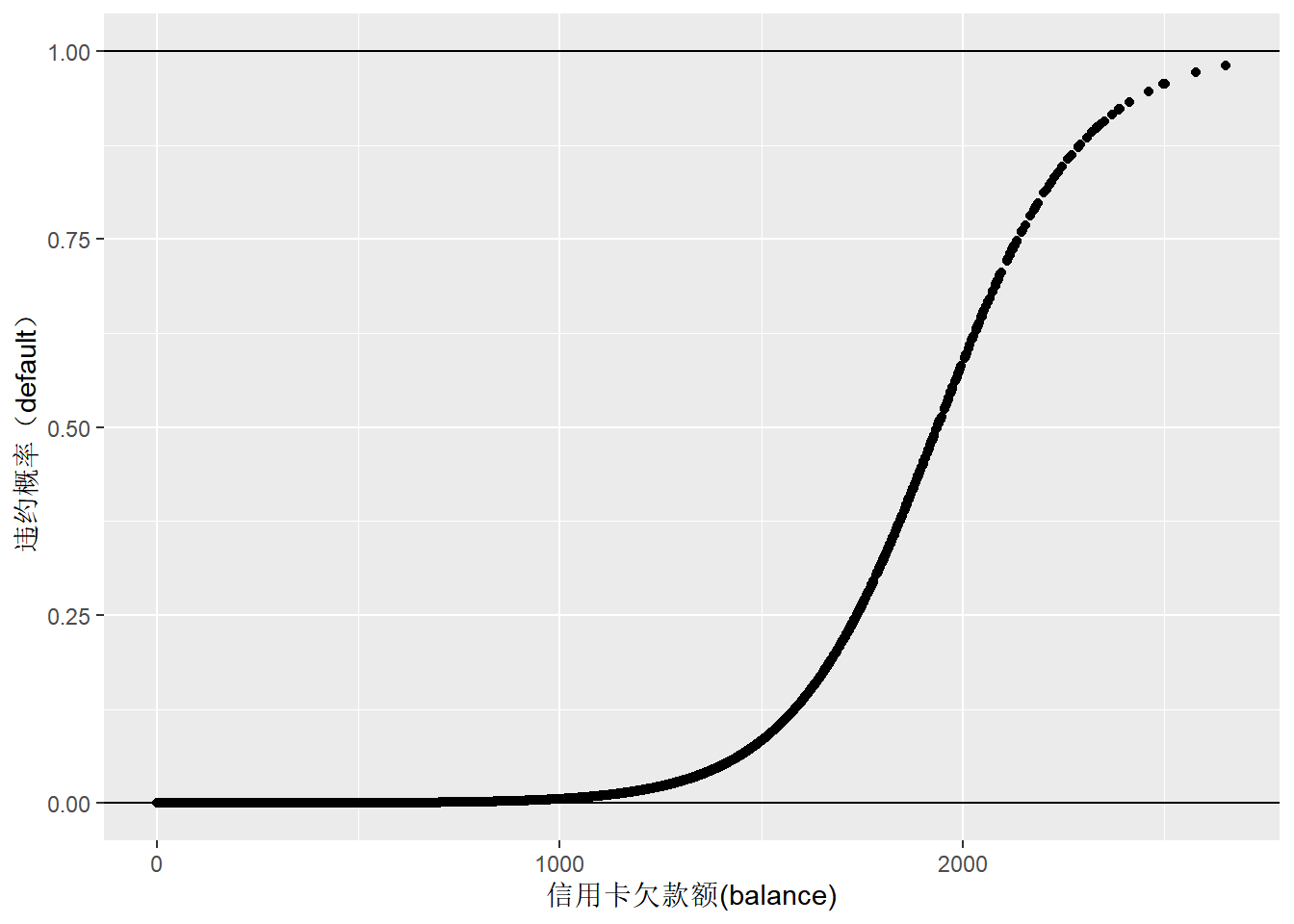
Figure 6: 信用卡欠款额与违约概率的logistic回归预测
手动计算信用卡还款违约概率来验证一下结果,与glm函数计算得到的概率是一致的:
x <- Default_dt$balance
y <- 1/(1+exp(-(-10.65+0.005499*x)))
default_fitted_dt <- data.table(x=Default_dt$balance, y=default_glm1$fitted.values)
ggplot(default_fitted_dt,aes(x,y)) + geom_point() +
geom_hline(yintercept = 0) + geom_hline(yintercept = 1) +
labs(y="违约概率(default)", x="信用卡欠款额(balance)") 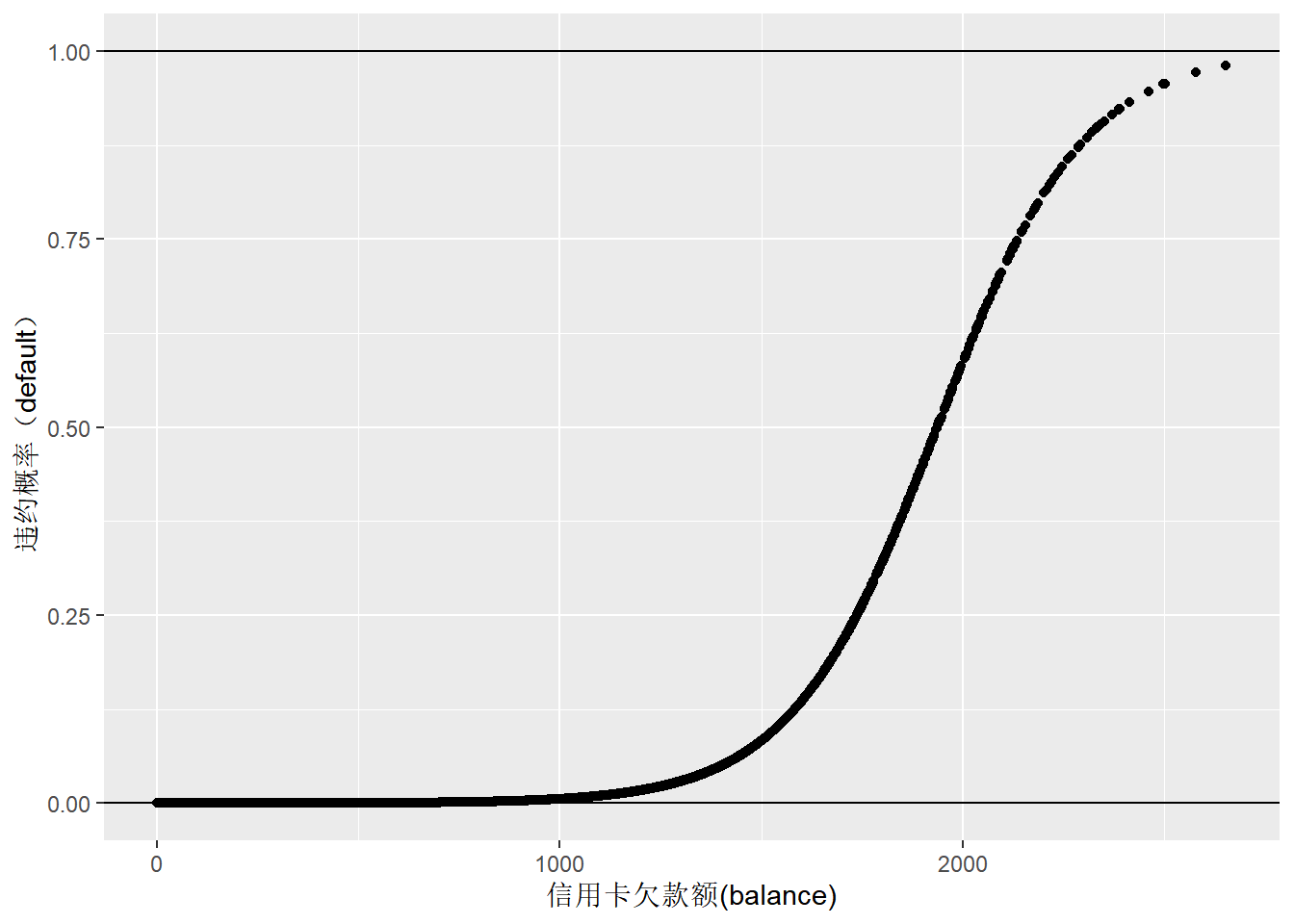
Figure 7: 信用卡欠款额与违约概率的logistic回归预测(手动计算)
2.3 连接函数(link function)和反向连接函数(inverse link function)
在ASReml说明书中,定义logit连接函数为: \[\eta=\frac{p}{1-p}\]
\[\eta=X\tau\] 感觉asreml说明书中的这个公式好像不对,正确的应该是: \[\eta=ln(\frac{p}{1-p})\]
反向连接函数定义为: \[p=\frac{1}{1+exp(-\eta)}\] 上边两个公式中,定义\(p\)为数据尺度(data scale),这里个人理解为事件发生概率值。而\(\eta\)指的是underlying scale,应该是基于\(\alpha+\beta x_{i}\)模型计算得到的结果。
个人感觉从反向连接函数到连接函数,理解起来更为顺畅。
2.4 针对多分类因变量(polytomous or multinomial variable)的转换
2.4.1 基线分类Logit模型(Baseline-Category Logit)
假设某个性状,如罗氏沼虾的大鳌,根据大小和颜色可以分为小鳌、老头虾蓝色、正常橙色、正常蓝色等无顺序的四种,分别编码为1, 2, 3, 4。 可以通过多变量logistic分布函数,把二分类logit模型扩展为多分类logit模型。
假设\(p_{ij}\)表示第\(i\)尾虾的大鳌属于第\(j\)个分类的概率,即\(p_{ij}=P(y_{i}=j)\),其中j=1,2,3,4。
引入基线或参考分类的概念,对应于二分变量时事件未发生的类别,建立处理方法。譬如大鳌颜色,如果把小鳌作为基线分类,那么可以据此计算其他3个类别的发生概率。
对于非基线类别j,发生的概率根据多变量logistic分布函数(反向连接函数)可以写为: \[ p_{ij} = \frac{e^{\alpha_{0j}+\beta_{1j}x_{i1}+\beta_{2j}x_{i2}+...+\beta_{kj}x_{ik}}}{1+\sum_{l\neq j^{*}} e^{\alpha_{0l}+\beta_{1l}x_{il}+\beta_{2l}x_{i2}+...+\beta_{kl}x_{ik}}} \] 上式中,\(j^{*}\)表示基线类别,\(x_{ik}\)表示第i个样本第k个自变量,\(\beta_{kj}\)表示第j个类别第k个自变量(解释变量)的回归系数。
因为所有类别的发生概率之和为1,\(\sum_{j=1}^{m}p_{j} = 1\),因此 ,对于基线变量\(j^{*}\),事件发生的概率为: \[ p_{ij^{*}} = 1-\sum_{l \neq j^{*}}p_{il} \\ =1-\frac{\sum_{l\neq j^{*}} e^{\alpha_{0l}+\beta_{1l}x_{il}+\beta_{2l}x_{i2}+...+\beta_{kl}x_{ik}}}{1+\sum_{l\neq j^{*}} e^{\alpha_{0l}+\beta_{1l}x_{il}+\beta_{2l}x_{i2}+...+\beta_{kl}x_{ik}}} \\ =\frac{1}{1+\sum_{l\neq j^{*}} e^{\alpha_{0l}+\beta_{1l}x_{il}+\beta_{2l}x_{i2}+...+\beta_{kl}x_{ik}}} \]
连接函数可以写为: \[ ln(\frac{p_{ij}}{p_{ij^{*}}})=\alpha_{0j}+\beta_{1j}x_{i1}+\beta_{2j}x_{i2}+...+\beta_{kj}x_{ik},\qquad j \neq j^{*} \]
譬如选择分类中第1个水平作为基线,公式写为: \[ln(\frac{p_{ij}}{p_{i1}})=\alpha_{0j}+\beta_{1j}x_{i1}+\beta_{2j}x_{i2}+...+\beta_{kj}x_{ik}\]
下边通过实例分析来加深对这部分内容的理解。数据为佛罗里达州四个湖共计219尾短吻鳄(Agresti )的主要食物来源。食物来源主要分为五类:鱼类(Fish)、无脊椎动物(Invertebrate)、爬行类(Reptile)、鸟(Bird)和其他(Other)。自变量包括湖、性别、鳄鱼规格。数据可以从这里下载。
数据按照自变量不同的组合分别统计。譬如在oklawaha湖中体长>2.3米的雌性短吻鳄,胃中食物为Invertebrate的1只,Bird的1只;在oklawaha湖中体长>2.3米的male短吻鳄,胃中食物为Fish的13只,Invertebrate的7只,Reptile的6只。
agresti_dt <- fread(input = "datasets/agresti.txt")
agresti_dt## profile Gender Size Lake Fish Invertebrate Reptile Bird Other
## 1: 1 f <2.3 george 3 9 1 0 1
## 2: 2 m <2.3 george 13 10 0 2 2
## 3: 3 f >2.3 george 8 1 0 0 1
## 4: 4 m >2.3 george 9 0 0 1 2
## 5: 5 f <2.3 hancock 16 3 2 2 3
## 6: 6 m <2.3 hancock 7 1 0 0 5
## 7: 7 f >2.3 hancock 3 0 1 2 3
## 8: 8 m >2.3 hancock 4 0 0 1 2
## 9: 9 f <2.3 oklawaha 3 9 1 0 2
## 10: 10 m <2.3 oklawaha 2 2 0 0 1
## 11: 11 f >2.3 oklawaha 0 1 0 1 0
## 12: 12 m >2.3 oklawaha 13 7 6 0 0
## 13: 13 f <2.3 trafford 2 4 1 1 4
## 14: 14 m <2.3 trafford 3 7 1 0 1
## 15: 15 f >2.3 trafford 0 1 0 0 0
## 16: 16 m >2.3 trafford 8 6 6 3 5定义短吻鳄胃中各种食物类别的发生概率:
- \(p_{1}\):Fish的概率;
- \(p_{2}\):Invertebrate的概率;
- \(p_{3}\):Reptile的概率;
- \(p_{4}\):Bird的概率;
- \(p_{5}\):Other的概率;
因为短吻鳄的主要食物是Fish,因此可以把它作为基底类。logit方程为: \[log(\frac{p_{ij}}{p_{i1}}) = \alpha_{0j}+\beta_{1j}x_{i1}+\beta_{2j}x_{i2}+\beta_{3j}x_{i3}...\] 对于j=2,3,4,5每个类别,需要估计的参数:
- 3个Lake水平
- 1个Gender水平
- 1个Size水平
加上截距,每个类别需要估计6个参数,四个类别共计24个参数。
设置每个自变量的参考水平。Lake:hancock;Gender:male;Size:<2.3。
cols_factor_v <- c("Lake","Gender","Size")
agresti_dt[, (cols_factor_v):=lapply(.SD, as.factor), .SDcols = cols_factor_v]
#set hancock as the base level for Lake
contrasts(agresti_dt$Lake) <- contr.treatment(levels(agresti_dt$Lake),base=2)
contrasts(agresti_dt$Lake)## george oklawaha trafford
## george 1 0 0
## hancock 0 0 0
## oklawaha 0 1 0
## trafford 0 0 1#set male as the base level for Gender
contrasts(agresti_dt$Gender) <- contr.treatment(levels(agresti_dt$Gender),base=2)
contrasts(agresti_dt$Gender)## f
## f 1
## m 0#set small size (<2.3) as the base level for Size
contrasts(agresti_dt$Size)=contr.treatment(levels(agresti_dt$Size),base=1)
contrasts(agresti_dt$Size)## >2.3
## <2.3 0
## >2.3 1利用vglm函数,建立logit模型进行分析。vglm函数默认cbind中最后一个类别即Fish作为基底或者参考类别。
multinomial_logit_m1 <- vglm(cbind(Bird,Invertebrate,Reptile,Other,Fish) ~ Lake + Size + Gender,family = multinomial, data=agresti_dt)
summary(multinomial_logit_m1)##
## Call:
## vglm(formula = cbind(Bird, Invertebrate, Reptile, Other, Fish) ~
## Lake + Size + Gender, family = multinomial, data = agresti_dt)
##
## Pearson residuals:
## Min 1Q Median 3Q Max
## log(mu[,1]/mu[,5]) -1.1985 -0.5478 -0.22421 0.3678 3.478
## log(mu[,2]/mu[,5]) -1.3218 -0.4611 0.01054 0.3810 1.866
## log(mu[,3]/mu[,5]) -0.7033 -0.5751 -0.35511 0.2610 2.064
## log(mu[,4]/mu[,5]) -1.6945 -0.2893 -0.10807 1.1236 1.367
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept):1 -2.4633 0.7739 NA NA
## (Intercept):2 -2.0745 0.6117 -3.392 0.000695 ***
## (Intercept):3 -2.9141 0.8856 NA NA
## (Intercept):4 -0.9167 0.4782 -1.917 0.055217 .
## Lakegeorge:1 -0.5753 0.7952 -0.723 0.469429
## Lakegeorge:2 1.7805 0.6232 2.857 0.004277 **
## Lakegeorge:3 -1.1295 1.1928 -0.947 0.343687
## Lakegeorge:4 -0.7666 0.5686 -1.348 0.177563
## Lakeoklawaha:1 -1.1256 1.1923 -0.944 0.345132
## Lakeoklawaha:2 2.6937 0.6693 4.025 5.70e-05 ***
## Lakeoklawaha:3 1.4008 0.8105 1.728 0.083926 .
## Lakeoklawaha:4 -0.7405 0.7421 -0.998 0.318372
## Laketrafford:1 0.6617 0.8461 0.782 0.434145
## Laketrafford:2 2.9363 0.6874 4.272 1.94e-05 ***
## Laketrafford:3 1.9316 0.8253 2.340 0.019263 *
## Laketrafford:4 0.7912 0.5879 1.346 0.178400
## Size>2.3:1 0.7302 0.6523 1.120 0.262918
## Size>2.3:2 -1.3363 0.4112 -3.250 0.001155 **
## Size>2.3:3 0.5570 0.6466 0.861 0.388977
## Size>2.3:4 -0.2906 0.4599 -0.632 0.527515
## Genderf:1 0.6064 0.6888 0.880 0.378666
## Genderf:2 0.4630 0.3955 1.171 0.241796
## Genderf:3 0.6276 0.6853 0.916 0.359785
## Genderf:4 0.2526 0.4663 0.542 0.588100
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Names of linear predictors: log(mu[,1]/mu[,5]), log(mu[,2]/mu[,5]),
## log(mu[,3]/mu[,5]), log(mu[,4]/mu[,5])
##
## Residual deviance: 50.2637 on 40 degrees of freedom
##
## Log-likelihood: -73.3221 on 40 degrees of freedom
##
## Number of Fisher scoring iterations: 5
##
## Warning: Hauck-Donner effect detected in the following estimate(s):
## '(Intercept):1', '(Intercept):3'
##
##
## Reference group is level 5 of the response从summary结果中可以看出,以Fish为基底类,针对其他四个类别分别建立了logit方程。每个方程需要求解6个参数,因此共解出了24个系数值。截距和3个自变量参考水平的系数值均为0,包括\(\alpha_{Food, Fish}=0\)、\(\beta_{Lake, hancock}=0\)、\(\beta_{Size,<2.3}=0\)、\(\beta_{Gender,male}=0\)。
四个logit方程的截距(Intercept)实际上给出的是在参考水平下(Lake=Hancock,size=small<2.3,Gender=male)的发生比对数值(log-odd)。譬如,在参考水平下,即Hancock湖小型雄性短尾鳄胃中食物Bird vs Fish的log-odd值为-1.94358,odd值为\(e^{-1.94358}\)=0.1431904。这表明在该湖中鱼类居多,鸟类较少。
如果从george湖捕获到一尾雌性短尾鳄,体长>2.3米,预测其胃中的食物类型Invertebrate vs Fish的发生比的自然对数值为(注意Invertebrate在系数中排名第二): \[ ln(\frac{p_{Invertebrate}}{p_{Fish}})=\alpha_{Invertebrate}+\beta_{Lake, George}+\beta_{Size,>2.3}+\beta_{Gender,female}) \\ =(-1.45492)+1.58417+(-1.36673)+0.19937 \\ =-1.03811 \]
发生比Odd为\(e^{-1.03811}\)=0.3541233。这表明,这尾短尾鳄胃中食物是Invertebrated的概率远低于是鱼的概率。
如果从trafford湖捕获到一尾雄性短尾鳄,体长<2.3米,预测其胃中的食物类型Invertebrate vs Fish的发生比的自然对数值为(注意Invertebrate在系数中排名第二): \[ ln(\frac{p_{Invertebrate}}{p_{Fish}})=\alpha_{Invertebrate}+\beta_{Lake, trafford}+\beta_{Size,<2.3}+\beta_{Gender,male}) \\ =(-1.45492)+2.47255+0+0 \\ =1.01763 \] 发生比Odd为\(e^{1.01763}\)=2.7666301。这表明,这尾短尾鳄胃中食物是Invertebrate的概率要高于是鱼的概率。
2.4.2 邻接分类Logit (Adjacent-category Logit)
在基线logit模型中,类别是无序的。现在考虑在分类是有序的情况下,该如何建立更为优化的模型。譬如对虾卵巢的发育等级,眼柄的磨损等级等性状,均为有序类别。对于无序分类,选择其中一个类别作为基线类。而对于有序分类,下边这样处理更有意义:
- 1 vs 2
- 2 vs 3
- 3 vs 4
- …
- r-1 vs r
2, 3, 4, …, r分别作为基线类。据此,可以建立r-1个邻接Logit方程(连接函数):
- \(L_{1} = ln(\frac{p_{1}}{p_{2}})\)
- \(L_{2} = ln(\frac{p_{2}}{p_{3}})\)
- …
- \(L_{r-1} = ln(\frac{p_{r-1}}{p_{r}})\)
其中\(L_{1}\)、\(L_{2}\)、…、\(L_{r-1}\)等进一步定义为由解释变量组成的方程:
- \(L_{1} = \alpha_{01}+\beta_{11}x_{1}+\beta_{21}x_{2}...+\beta_{k1}x_{k}\)
- \(L_{2} = \alpha_{02}+\beta_{12}x_{1}+\beta_{22}x_{2}...+\beta_{k2}x_{k}\)
- …
- \(L_{r-1} = \alpha_{0,r-1}+\beta_{1,r-1}x_{1}+\beta_{2,r-1}x_{2}...+\beta_{k,r-1}x_{k}\)
\(L_{1}\)到\(L_{r-1}\)之间可以相互组合,构建不同的logit方程,譬如:
\[ ln(\frac{p_{3}}{p_{1}}) = -L_{2}-L_{1} \] 这是因为: \[ ln(\frac{p_{1}}{p_{2}}) = L_{1} \\ \frac{p_{1}}{p_{2}} = e^{L_{1}} \\ \frac{p_{2}}{p_{1}} = \frac{1}{e^{L_{1}}} \\ \frac{p_{2}}{p_{1}} = e^{-L_{1}} \\ ln(\frac{p_{2}}{p_{1}}) = -L_{1} \\ \] 类似: \[ ln(\frac{p_{2}}{p_{3}}) = L_{2} \\ ln(\frac{p_{3}}{p_{2}}) = -L_{2} \\ \] 所以 \[ ln(\frac{p_{3}}{p_{1}}) = ln(\frac{p_{3}}{p_{2}}\frac{p_{2}}{p_{1}}) \\ = ln(\frac{p_{3}}{p_{2}}) + ln(\frac{p_{2}}{p_{1}}) \\ = -L_{2}-L_{1} \] 由此可以推测: \[ ln(\frac{p_{r}}{p_{1}}) = ln(\frac{p_{r}}{p_{r-1}}\frac{p_{r-1}}{p_{r-2}}...\frac{p_{2}}{p_{1}}) \\ = ln(\frac{p_{r}}{p_{r-1}}) + ln(\frac{p_{r-1}}{p_{r-2}})+...+ln(\frac{p_{2}}{p_{1}}) \\ = -L_{r-1}-L_{r-2}+...-L_{1} \] 上述公示表明,邻接logit模型可以组合构建基线logit模型。
2.4.3 The proportional-Odds Cumulative Logit Model (百分比发生比累积Logit模型)
这个模型可能是有序分类最为常用的模型。ASReml中好像用的也是这个模型。
假设分类变量\(y=1,2,3,...,r\),每个类别发生的概率分别为\(p_{1}, p_{2},...,p_{r}\),并且\(P(y_{i} \le r)=p_{1} + p_{2} + ... + p_{r}\)。
假定存在一个隐藏变量(latent variable)\(y^{*}\),与解释变量\(x\)之间存在一种线性关系: \[ y_{i}^{*} = \alpha+\beta_{1} x_{i1}+...+\beta_{k} x_{ik}+\varepsilon_{i} \] 如果是二分变量,\(y_{i}^{*}\)划分为2个区域;如果是多分类,那么会被划分为r个区域,有r-1个边界阈值。设定r-1个边界阈值为:\(\alpha_{1}<\alpha_{2}<\alpha_{3}...<\alpha_{r-1}\),分类变量的值为:
\[ y_{i} = \left\{\begin{matrix} 1 & y_{i}^{*} \le \alpha_{1} \\ 2 & \alpha_{1} < y_{i}^{*} \le \alpha_{2} \\ ... \\ r-1 & \alpha_{r-2} < y_{i}^{*} \le \alpha_{r-1} \\ r & \alpha_{r-1} < y_{i}^{*} \le \alpha_{r} \end{matrix}\right. \] 依据上述设定,\(y_{i} \le j\)(\(j=1,2,3...,r-1\))的概率为: \[ P(y_{i} \le j) = P(y_{i}^{*} \le \alpha_{j}) \\ = P(\alpha+\beta_{1} x_{i1}+...+\beta_{k} x_{ik}+\varepsilon_{i} \le \alpha_{r})) \\ = P(\varepsilon_{i} \le \alpha_{j}-(\alpha+\beta_{1} x_{i1}+...+\beta_{k} x_{ik})) \\ \] 其中\(y_{i}\)表示第i个样本落在1到j类别之间的概率。假定残差项\(\varepsilon\)独立分布,符合logistic或者标准正态分布,上式实际上为累积分布函数。
如果残差项\(\varepsilon\)符合logistic分布,那么logit模型为: \[ ln(\frac{P(y_{i} \le j)}{P(y_{i} > j)}) \\ = \alpha_{j}-(\alpha+\beta_{1} x_{i1}+...+\beta_{k} x_{ik}) \\ = \alpha_{j} - \alpha -\beta_{1} x_{i1}-...-\beta_{k} x_{ik} \] 反之: \[ ln(\frac{P(y_{i} > j)}{P(y_{i} \le j)}) \\ = -(\alpha_{j} - \alpha -\beta_{1} x_{i1}-...-\beta_{k} x_{ik}) \\ = \alpha-\alpha_{j}+\beta_{1} x_{i1}+...+\beta_{k} x_{ik} \]
上述公式跟二分变量很相似。假设分类变量\(j=1, 2, 3, 4, ..., r\),那么logit模型为: \[ L_{1} = logit(P(y_{i} \le 1)) = ln(\frac{y_{i} \le 1}{y_{i} > 1}) = \alpha_{1} - \alpha - \beta_{1} x_{i1} - ... - \beta_{k} x_{ik} \\ L_{2} = logit(P(y_{i} \le 2)) = ln(\frac{y_{i} \le 2}{y_{i} > 2}) = \alpha_{2} - \alpha - \beta_{1} x_{i1} - ... - \beta_{k} x_{ik} \\ L_{3} = logit(P(y_{i} \le 3)) = ln(\frac{y_{i} \le 3}{y_{i} > 3}) = \alpha_{3} - \alpha - \beta_{1} x_{i1} - ... - \beta_{k} x_{ik} \\ ... \\ L_{r-1} = logit(P(y_{i} \le r-1)) = ln(\frac{y_{i} \le r-1}{y_{i} > r-1}) = \alpha_{r-1} - \alpha - \beta_{1} x_{i1} - ... - \beta_{k} x_{ik} \\ \] 注意\(L_{1}, L_{2},...,L_{r-1}\)是累积发生比。
上述logit方程的几个特点:
- 所有logit回归方程的斜率都是一样的,即不同logit方程具有相同的一套\(\beta\)值,差别仅在截距上。 因此logit回归曲线在垂直方向上是平行的。猜想这主要是因为\(L_{r}\)包括\(L_{r-1},...,\)\(L_{3}\)包括\(L_{2}\),因此它们的斜率是一样的。
- 当两个logit方程右手边的解释变量x,取相同的水平值时,两个方程logit-odd值的差异仅在截距上,譬如类别\(j\)和\(j^{'}\),logit-odd差值为\(\alpha_{j}-\alpha_{j^{'}}\)。因此,不同类别log-odd值之间,是成比例的。因此,有序logit模型也称为百分比发生比模型(proportional-odds model)。与基线分类Logit模型相比,本模型要估计的参数大幅度降低,所有的logit模型共享一套与解释变量相关的回归系数。
- 总共有k+1+r-1=k+r个参数需要估计,即回归系数\(\beta\)和不同类别的阈值\(\alpha_{j}\)。如果是固定效应,这里k指的是一个处理的水平数;如果有两个固定效应,水平数分别为k和i,那么需要估计的参数应该是k+i+r。
- 既然所有的logit方程都有一个共同的常数\(\alpha\),为了简化方程,可以将其设置为0。因此logit方程可简化为\(logit(P(y_{i} \le j)) = ln(\frac{P(y_{i} \le j)}{P(y_{i} > j)})= \alpha_{j} -\beta_{1} x_{i1}-...-\beta_{k} x_{ik}\)
下边以四种奶酪的口味评分数据进行实例分析。一共有四种奶酪,评分为1-9级。
cheese_dt <- fread(input="datasets/cheese.txt",header = FALSE)
colnames(cheese_dt) <- c("Cheese",paste("S",as.character(seq(1,9)),sep=""),"Total")
cheese_dt## Cheese S1 S2 S3 S4 S5 S6 S7 S8 S9 Total
## 1: A 0 0 1 7 8 8 19 8 1 52
## 2: B 6 9 12 11 7 6 1 0 0 52
## 3: C 1 1 6 8 23 7 5 1 0 52
## 4: D 0 0 0 1 3 7 14 16 11 52利用MASS包中的polr()函数进行proportional-odds model分析。
cheese_dt[,Total:=NULL]
cheese_melt_dt <- melt.data.table(cheese_dt,id.vars = c("Cheese"),variable.name = c("Taste"), value.name = "N")
#Taste需要是因子类型
result <- polr(Taste ~ Cheese, weights = N, data = cheese_melt_dt)
summary(result)##
## Re-fitting to get Hessian## Call:
## polr(formula = Taste ~ Cheese, data = cheese_melt_dt, weights = N)
##
## Coefficients:
## Value Std. Error t value
## CheeseB -3.352 0.4287 -7.819
## CheeseC -1.710 0.3715 -4.603
## CheeseD 1.613 0.3805 4.238
##
## Intercepts:
## Value Std. Error t value
## S1|S2 -5.4674 0.5236 -10.4413
## S2|S3 -4.4122 0.4278 -10.3148
## S3|S4 -3.3126 0.3700 -8.9522
## S4|S5 -2.2440 0.3267 -6.8680
## S5|S6 -0.9078 0.2833 -3.2037
## S6|S7 0.0443 0.2646 0.1673
## S7|S8 1.5459 0.3017 5.1244
## S8|S9 3.1058 0.4057 7.6547
##
## Residual Deviance: 711.3479
## AIC: 733.3479截距(Intercept)可以认为是不同类别的阈值,即\(\alpha_{j}\)。
根据计算结果,如果想知道奶酪B好吃度落在1-6级的发生比: \[ logit(P(y_{i} \le 6)) = ln(\frac{P(y_{i} \le 6)}{P(y_{i} > 6)})= \alpha_{6} -\beta_{2} x_{i2} \\ = 0.0443-(-3.352)=3.3963 \] 发生比为\(e^{3.3963}\)=29.8534377。发生比数值非常大,这表明奶酪B不好吃的概率非常大。这跟数据也是相符的。
如果想知道奶酪A好吃度落在1-6级的发生比: \[ logit(P(y_{i} \le 6)) = ln(\frac{P(y_{i} \le 6)}{P(y_{i} > 6)})= \alpha_{6} -\beta_{1} x_{i1} \\ = 0.0443-(0)=0.0443 \] 发生比为\(e^{0.0443}\)=1.0452959。发生比数值远小于奶酪B,这表明奶酪A好吃度落在1-6级的可能性不大,好吃的概率非常大。这跟数据也是相符的。
利用ASREML分析,给出的结果为:
Model_Term Level Effect seEffect
Cheese A 0.000 0.000
Cheese B 3.352 0.4235
Cheese C 1.710 0.3731
Cheese D -1.613 0.3778
Trait 1 -5.467 0.5202
Trait 2 -4.412 0.4247
Trait 3 -3.313 0.3697
Trait 4 -2.244 0.3262
Trait 5 -0.9078 0.2748
Trait 6 0.4425E-01 0.2598
Trait 7 1.546 0.3042
Trait 8 3.106 0.4044
Trait分别对应的值即是8个阈值,与plor()的计算结果也是一致的。但是四种Cheese的固定效应,跟利用plor的计算结果正好是相反的。推测,ASReml直接把模型泛写为\(logit(P(y_{i} \le j)) = ln(\frac{P(y_{i} \le j)}{P(y_{i} > j)})= \alpha_{j} + \beta_{1} x_{i1} +...+\beta_{k} x_{ik}\)这种形式了。
进一步推导出反向连接函数: \[ \frac{P(y_{i} \le j)}{P(y_{i} > j)} = e^{\alpha_{j}-(\alpha+\beta_{1} x_{i1}+...+\beta_{k} x_{ik})} \\ \frac{P(y_{i} \le j)}{1-P(y_{i} \le j)} = e^{\alpha_{j}-(\alpha+\beta_{1} x_{i1}+...+\beta_{k} x_{ik})} \\ P(y_{i} \le j) = e^{\alpha_{j}-(\alpha+\beta_{1} x_{i1}+...+\beta_{k} x_{ik})} - P(y_{i} \le j)e^{\alpha_{j}-(\alpha+\beta_{1}x_{i1}+...+\beta_{k} x_{ik})} \\ P(y_{i} \le j) + P(y_{i} \le j)e^{\alpha_{j}-(\alpha+\beta_{1}x_{i1}+...+\beta_{k} x_{ik})}= e^{\alpha_{j}-(\alpha+\beta_{1}x_{i1}+...+\beta_{k} x_{ik})} \\\ P(y_{i} \le j)(1 + e^{\alpha_{j}-(\alpha+\beta_{1}x_{i1}+...+\beta_{k} x_{ik})}) = e^{\alpha_{j}-(\alpha+\beta_{1} x_{i1}+...+\beta_{k} x_{ik})} \\ P(y_{i} \le j) = \frac{e^{\alpha_{j}-(\alpha+\beta_{1} x_{i1}+...+\beta_{k} x_{ik})}}{1 + e^{\alpha_{j}-(\alpha+\beta_{1}x_{i1}+...+\beta_{k} x_{ik})}} \]
2.5 Probit转换
Probit模型是另外一种把模型与概率连接在一起的函数。Probit模型实际上是与正态分布紧密相关的。正态分布曲线,也就是钟形曲线,应该是非常熟悉的,在生物统计学教程中也会经常见到。生成1000个符合标准正态分布的数值,标准差为1,平均值为0。
#生成符合正态分布的随机数
x = rnorm(1000)
#根据概率密度函数,获得x对应的概率密度
y = dnorm(x)
#画出标准正态分布曲线
xy = data.table(x,y)
ggplot(data = xy, aes(x,y)) + geom_point()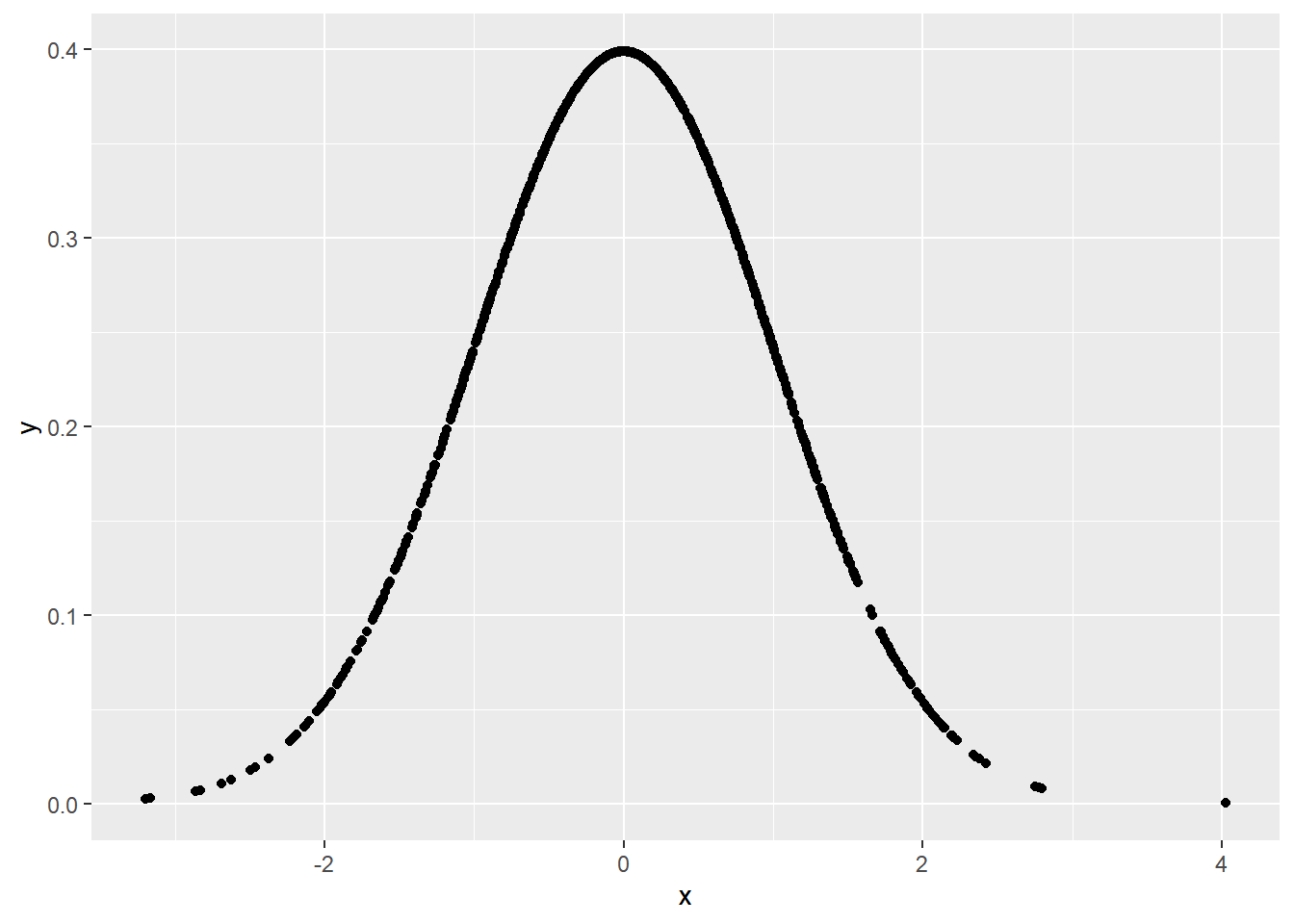
Figure 8: 正态分布曲线
正态分布的概率密度(PDF)函数为: \[ f(x) = \frac{1}{\sigma \sqrt{2\pi}}e^{-\frac{(x-\mu)^{2}}{2\sigma^{2}}} \] 其中\(\mu\)为均值,\(\sigma\)为标准差。如前所述,概率密度函数是为了计算连续变量落在某个区间的概率而产生的一个概念,因此具有以下三个性质:
- \(f(x) \ge 0\)
- \(\int_{-\infty}^{\infty}f(x)dx = 1\)
- \(P(a < x \le b) = \int_{a}^{b}f(x)dx\)
对于x=0,其概率密度函数值f(x=0)=0.3989423;f(x=2)=0.053991。随机变量取每个具体值的概率为0,但落在每一点处的概率是有相对大小的。x落在0处的概率要大于x落在2处的概率。
正态分布的累积分布函数为: \[F(x) = \frac{1}{\sigma\sqrt{2\pi}}\int_{-\infty}^{x}e^{-\frac{(t-\mu)^{2}}{2\sigma^{2}}}dt\]
z = pnorm(x)
xz = data.table(x,z)
ggplot(data = xz, aes(x, z)) + geom_point() + geom_hline(yintercept = 0) + geom_hline(yintercept = 1)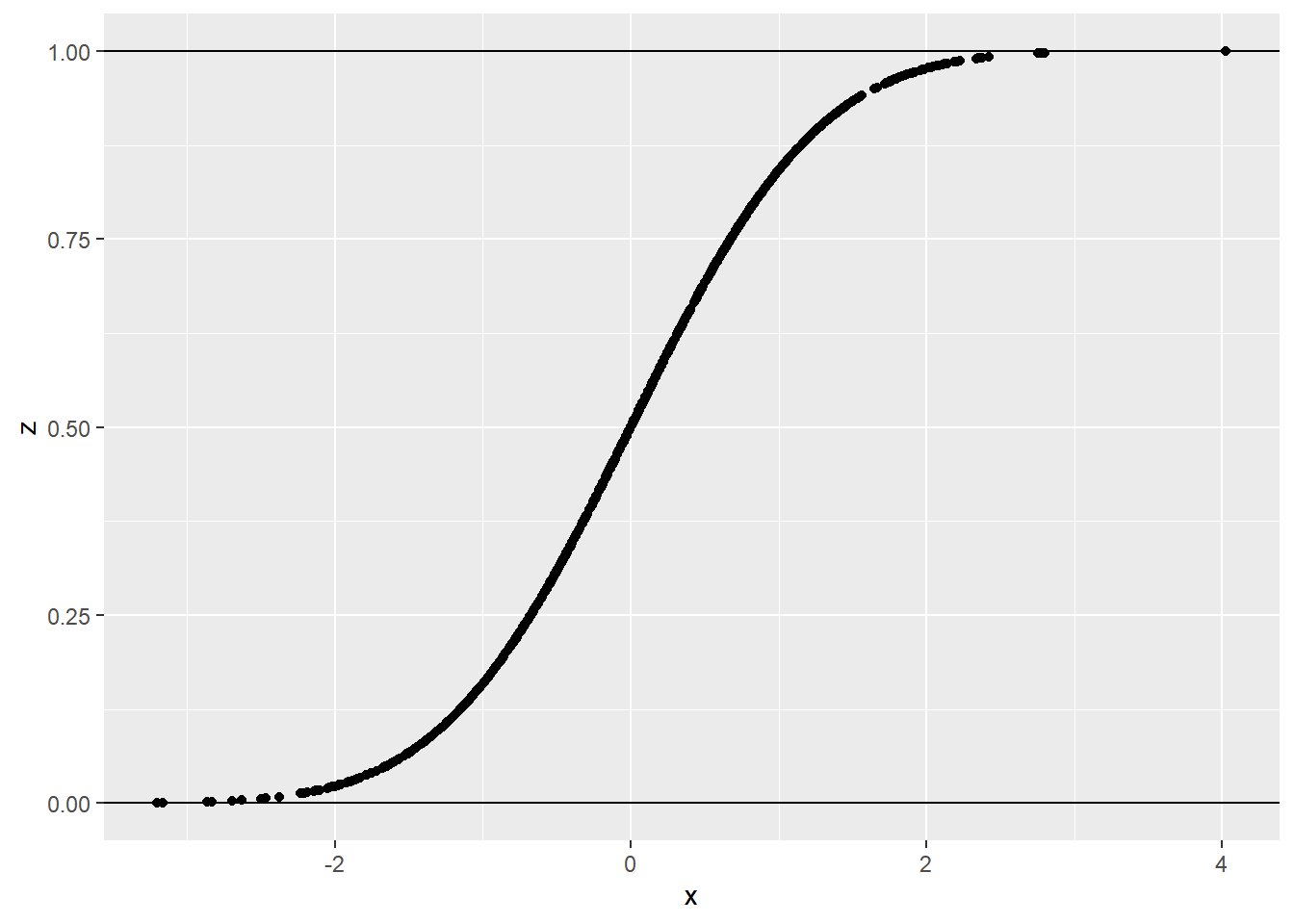
Figure 9: 正态累积分布函数
正态累积分布函数,满足了在2.1部分提到的转换三原则。
因此,对于一个二项分布,反向连接函数公式可以表述为: \[p_{i} = F(\alpha+\beta x_{i})= \frac{1}{\sigma\sqrt{2\pi}}\int_{-\infty}^{\alpha+\beta x_{i}}e^{-\frac{(t-\mu)^{2}}{2\sigma^{2}}}dt\]
标准正态累积分布函数,指的是平均值为0,标准差为1时的分布函数,记为\(\Phi\): \[p_{i} = \Phi(\alpha+\beta x_{i}) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\alpha+\beta x_{i}}e^{-\frac{t^{2}}{2}}dt\]
probit连接函数为: \[ \alpha+\beta x_{i} = \Phi^{-1}(p) \]
利用probit连接函数,分析信用卡违约数据:
default_glm2 <- glm(default_num ~ balance, family = binomial(link = "probit"), data=Default_dt)
summary(default_glm2)##
## Call:
## glm(formula = default_num ~ balance, family = binomial(link = "probit"),
## data = Default_dt)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.0208 -0.1399 -0.0348 -0.0051 4.1690
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -5.3539053 0.1697473 -31.54 <2e-16 ***
## balance 0.0027107 0.0001088 24.91 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 2920.6 on 9999 degrees of freedom
## Residual deviance: 1605.5 on 9998 degrees of freedom
## AIC: 1609.5
##
## Number of Fisher Scoring iterations: 8default_glm2_fitted_dt <- data.table(x=Default_dt$balance, y=default_glm2$fitted.values)
ggplot(default_glm2_fitted_dt, aes(x,y)) + geom_point() +
geom_hline(yintercept = 0) + geom_hline(yintercept = 1) +
labs(y="违约概率(default)", x="信用卡欠款额(balance)") 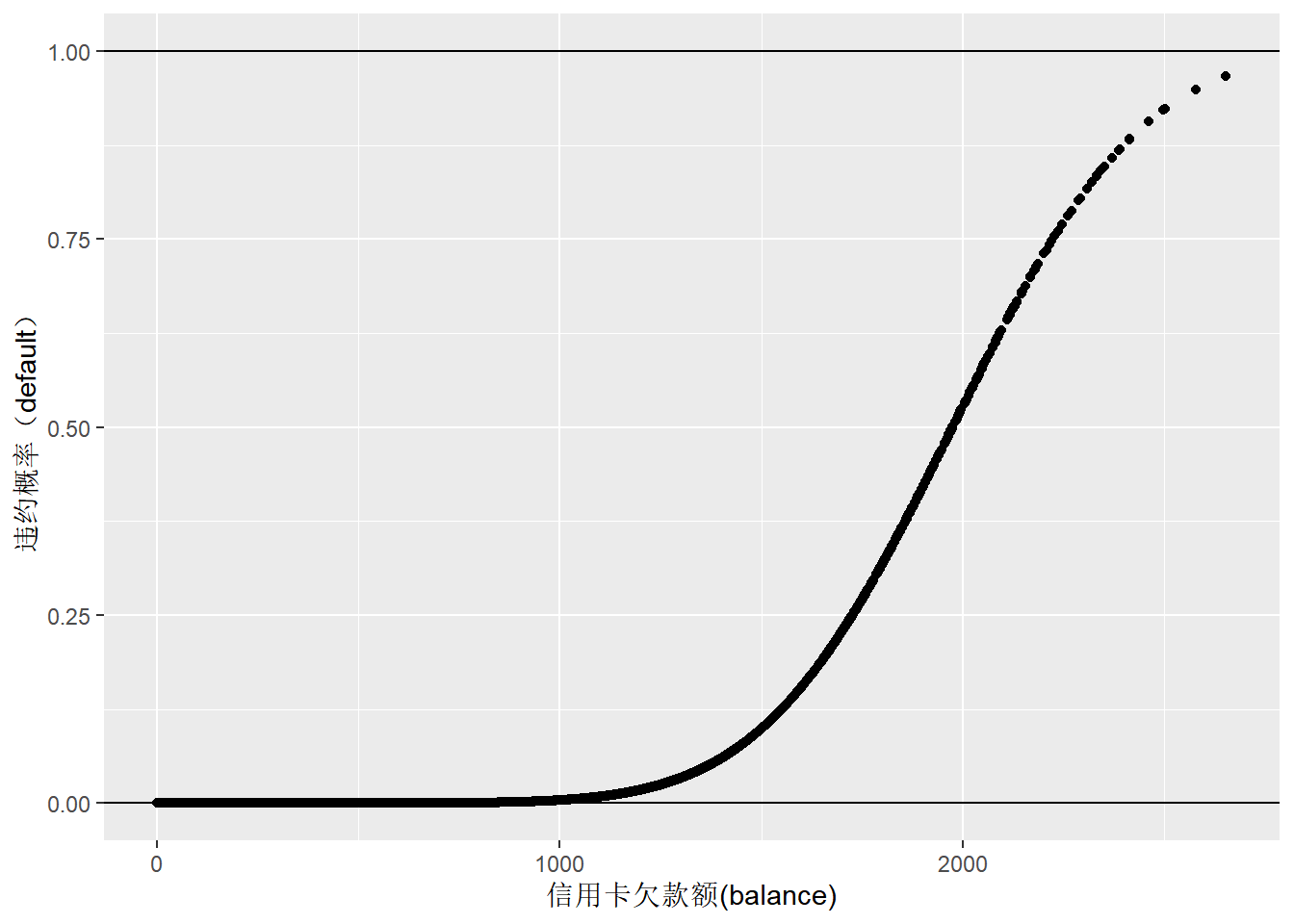
Figure 10: 信用卡欠款额与违约概率的logistic回归预测
手动计算得到的结果与glm函数的结果存在一定差异,需要进一步查询资料,搞清楚glm函数中probit的计算过程。
z = -5.3539053 + 0.0027107*(Default_dt$balance)
z_mean <- mean(z)
z_sigma <- sd(z)
z_new <- (z - z_mean)/z_sigma
default_fitted_validation_dt <- data.table(x=Default_dt$balance, y=pnorm(z_new))
ggplot(default_fitted_validation_dt, aes(x,y)) + geom_point() +
geom_hline(yintercept = 0) + geom_hline(yintercept = 1) +
labs(y="违约概率(default)", x="信用卡欠款额(balance)") 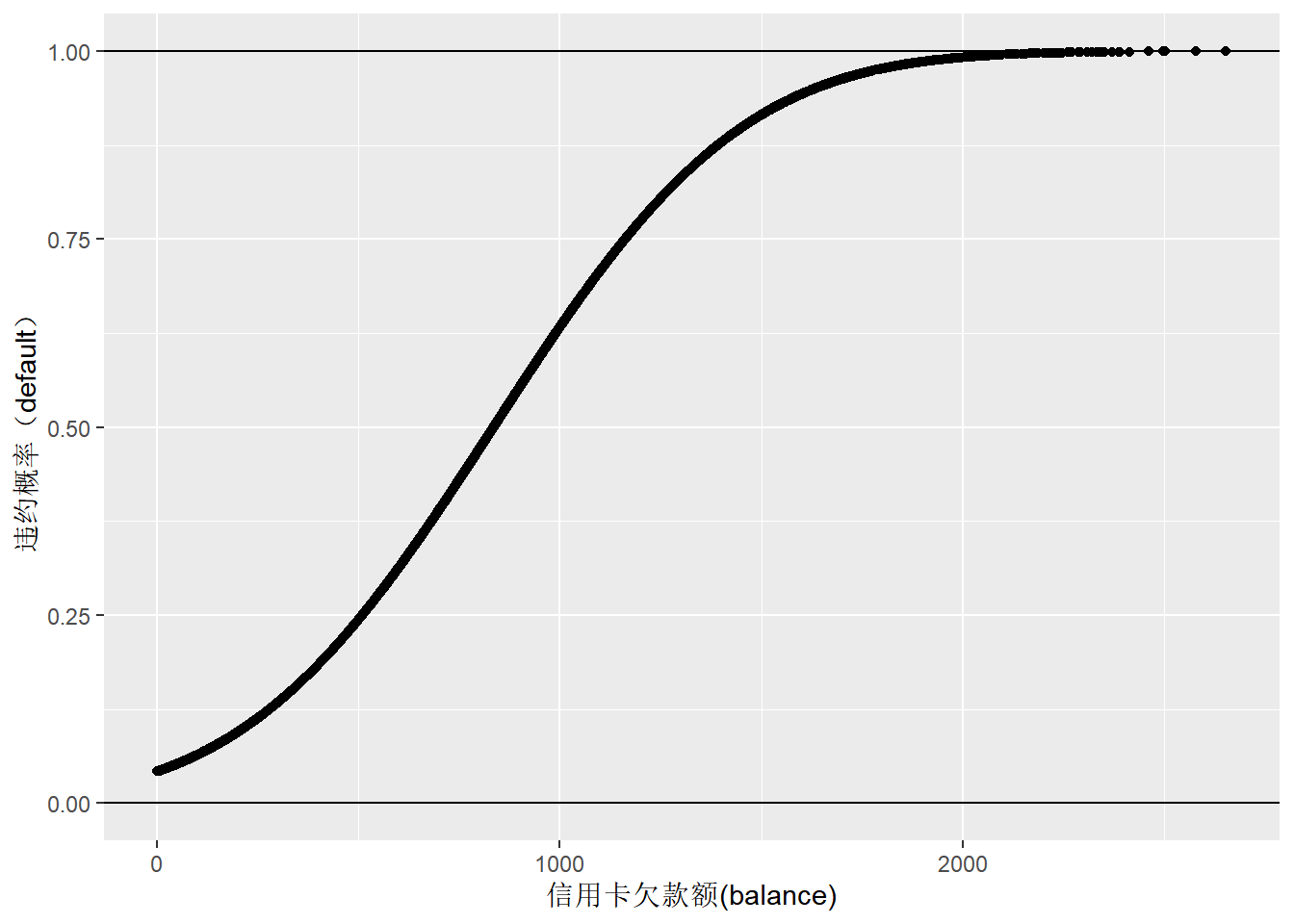
Figure 11: 信用卡欠款额与违约概率的logistic回归预测(手动验证)