How to convert binary to decimalism

今天跟儿子讨论，如何把二进制转换为十进制。二进制的规则是逢二进一，借一当二。我们写了一下0到9的二进制表示方法，也找到了转换方法。

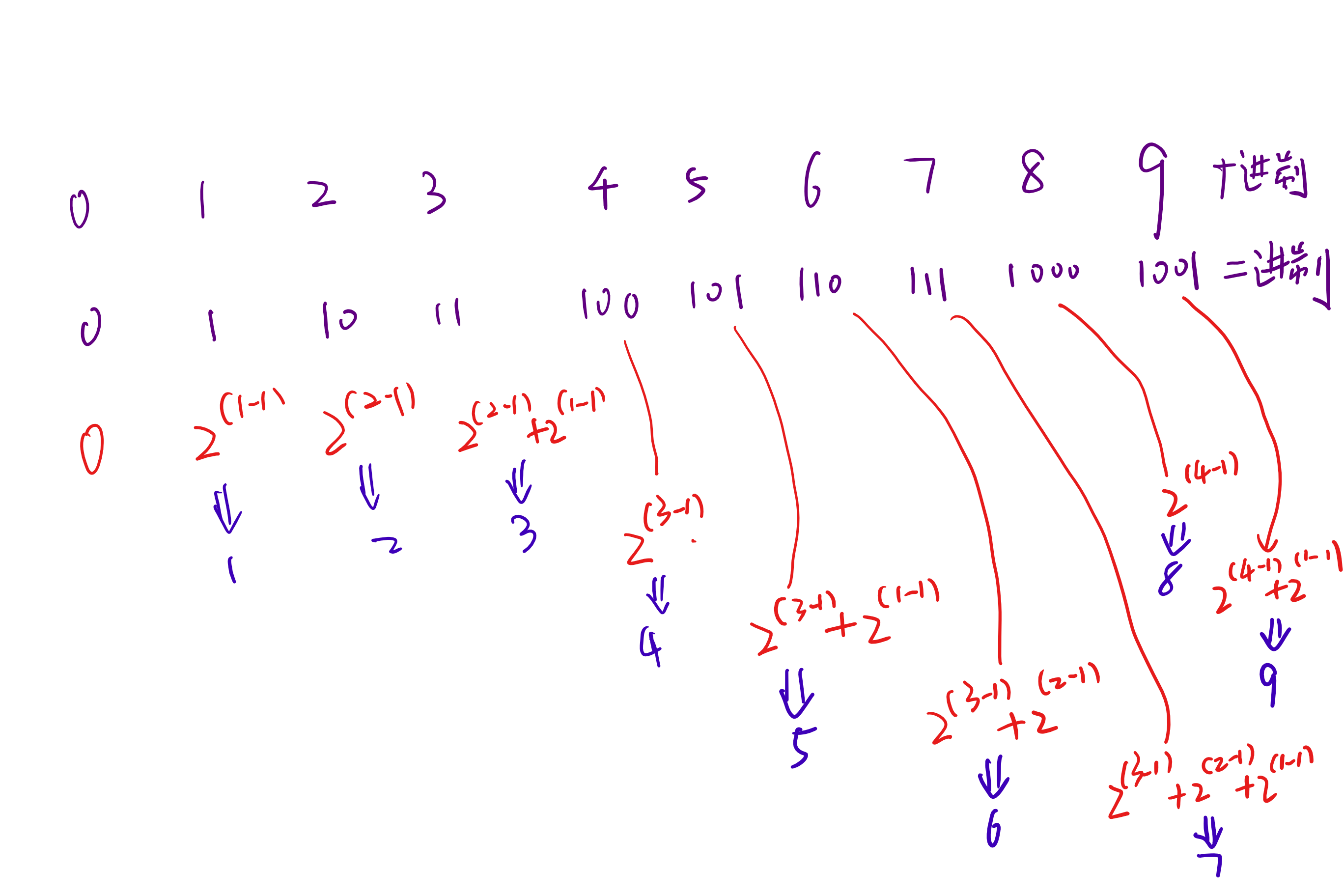
封装了一个函数：

bin2dec <- function(x) {
  n <- nchar(x)
  sum <- 0
  x_split <- rev(unlist(strsplit(x,split = "")))
  for (i in 1:n) {
    if(x_split[i] == 1) {
      sum <- sum + 2^(i-1)
    }
  }
  return(sum)
}

测试一下: c++中的short int 即16个bit可以表示的最大十进制数为：

bin_str <- paste(rep("1",16),collapse = "")
print(bin_str)

## [1] "1111111111111111"

print(bin2dec(bin_str))

## [1] 65535

但是在教科书中，我们通常看到，short int的取值范围在-32768 ~ 32767。这是因为在进行二进制计算时，需拿出最左边的一位用于表示正负符号，1表示负号。因此实际可用的位数就变为了15位。 计算机二进制的表示方法有三种：原码，反码和补码。

对于正数，反码和补码跟原码是一样的。

对于负数，反码是指原码除了符号位不变，其余各位1 -> 0,0 -> 1；补码，是在反码的基础上加1。如下图所示：

计算机在计算时，通常只会执行加法操作，减法通常也会转换为加法，而且为了加快计算速度，符号位也需要直接参与计算。从上图中可以看到，如果符号位直接参与计算，利用原码得到的计算结果是错误的。而利用反码，会得到-0，这意味着0有正负两种形式。而利用补码，可以得到正确的值。

继续看下边的例子，有一个更深刻的印象：

进一步的解释，参见下述链接：https://blog.csdn.net/wo17fang/article/details/52241682。

讨论一个问题： 对于8个bit位，如果拿出第8位，用来表示正负号，那么实际上可用的位数只有7位，用来表示的最大正整数为“1111111”，十进制为127：

print(bin2dec("1111111"))

## [1] 127

据此推测，可表示的最大负数应该是-127。但是，在书本上通常会看到，最大可表示的负数为-128，这主要是补码的功劳：

(-1) + (-127) = [1000 0001]原 + [1111 1111]原 = [1111 1111]补 + [1000 0001]补 = [1000 0000]补

因此用补码可以表示-128 ~ 172，而利用原码只可以表示-127 ~ 127。多出的这一位，实际上是利用原来的-0，来表示的。