比较同一处理不同水平的差异,譬如不同养殖密度、不同饲料对生长速度的影响,经常会用到方差分析的方法。而在方差分析中,自由度是一个非常重要的概念。这篇博客记录对这两个概念的理解。
1. 自由度
自由度(Degrees of freedom)是统计学上最经常见到的一个概念。关于它的概念,第一次接触,理解起来有些困难。维基百科的解释是这样的: “In statistics, the number of degrees of freedom is the number of values in the final calculation of a statistic that are free to vary”。试着翻译:“在统计学中,自由度的个数被定义为,在一个统计参数的计算过程中,可以自由变化的数值的个数”。
维基百科中,以方差为例,试着给出自由度的计算方法。
In general, the degrees of freedom of an estimate of a parameter are equal to the number of independent scores that go into the estimate minus the number of parameters used as intermediate steps in the estimation of the parameter itself (e.g. the sample variance has N − 1 degrees of freedom, since it is computed from N random scores minus the only 1 parameter estimated as intermediate step, which is the sample mean).
翻译:一般来讲,一个参数估计值的自由度等于, 在估计过程中使用的独立样本(score)个数,减掉中间步骤中用到的参数个数。以方差为例,它的自由度为N-1,是因为计算方需要n个独立样本值,而在中间计算过程中用到了样本均值这个参数,所以自由度为n-1。
方差的计算公式:
\[Var(Y) =\frac{\sum_{i=1}^{n} (y_{i}-\bar{y})^{2}}{n-1}\]
结合百度百科关于方差自由度的解释,感觉可以这样理解:
- 首先,在估计总体的平均数时,由于样本中的 n 个数都是相互独立的,从其中抽出任何一个数都不影响其他数据,所以其自由度为n。
- 在估计总体的方差时,使用的是离差平方和。由上面的公式可知,计算方差需要首先获得n个数的平均值。一旦平均数确定了,那么在计算方差时,只要n-1个数的离差平方和确定了,方差也就确定了;因为在均值确定后,如果知道了其中n-1个数的值,第n个数的值也就确定了。这里,均值就相当于一个限制条件,由于加了这个限制条件,估计总体方差的自由度为n-1。
- 例如,我们有5尾虾的体重数据(n=5),想估计其方差。计算得到5尾虾的平均值为\(\mu\)=20g,那么方差就会即受到\(\mu\)=20g的条件限制。因为随机选择4尾虾18g、22g、23g、17g计算得到离差平方和后,第5尾虾的体重,根据均值可以算出来,它的离差平方和也就确定了。因而自由度df=n-1=5-1=4,这表示第5尾虾的离差是依赖平均数,受到平均数限制的。推而广之,任何统计量的自由度df=n-k(k为限制条件的个数)。
知乎上关于自由度的解释非常专业,建议前往理解和学习,有一些非常难以理解。答主Wang Sigma的一句话,是我能够理解的“本质上,自由度是做一个估计(推测)时,所拥有的独立信息(证据)的数量”。
方差分析,需要用到自由度,下边结合方差分析,来研究自由度的变化。
2. 方差分析(analysis of variance,ANOVA)
在育种工作中,我们经常会通过各种试验来分析不同的因素对试验结果的影响。譬如设计实验,分析不同养殖密度、不同饲料种类对生长速度的影响,找出最好的那个水平。
ANOVA分析,可以用来实现上述目的。主要是用来检测分类变量的效应,也就是我们在线性混合效应模型中常说的固定效应。譬如不同性别、不同群体的差异。
2.1 生成数据
我们同样以对虾为例,生成投喂四种饲料后的体重数据。饲料种类称为一个处理,每种饲料是一个水平。
require(data.table)
require(ggplot2)
feed.1 <- rnorm(n=100,mean = 25,sd = 6)
feed.2 <- rnorm(n=100,mean = 20,sd = 6)
feed.3 <- rnorm(n=100,mean = 15,sd = 6)
feed.4 <- rnorm(n=100,mean = 10,sd = 6)
feed <- data.table(F1=feed.1,F2=feed.2,F3=feed.3,F4=feed.4)
feed.new <- melt(feed,measure.vars = 1:4)
setnames(feed.new,colnames(feed.new),c("Feed","Weight"))
ggplot(data=feed.new,aes(x=Feed,y=Weight,color=Feed)) +
geom_boxplot(outlier.size = 0)+
geom_jitter(alpha=0.3)+
labs(x="饲料种类",y="体重")+
theme_gray(base_size = 20)+
theme(legend.position = "none")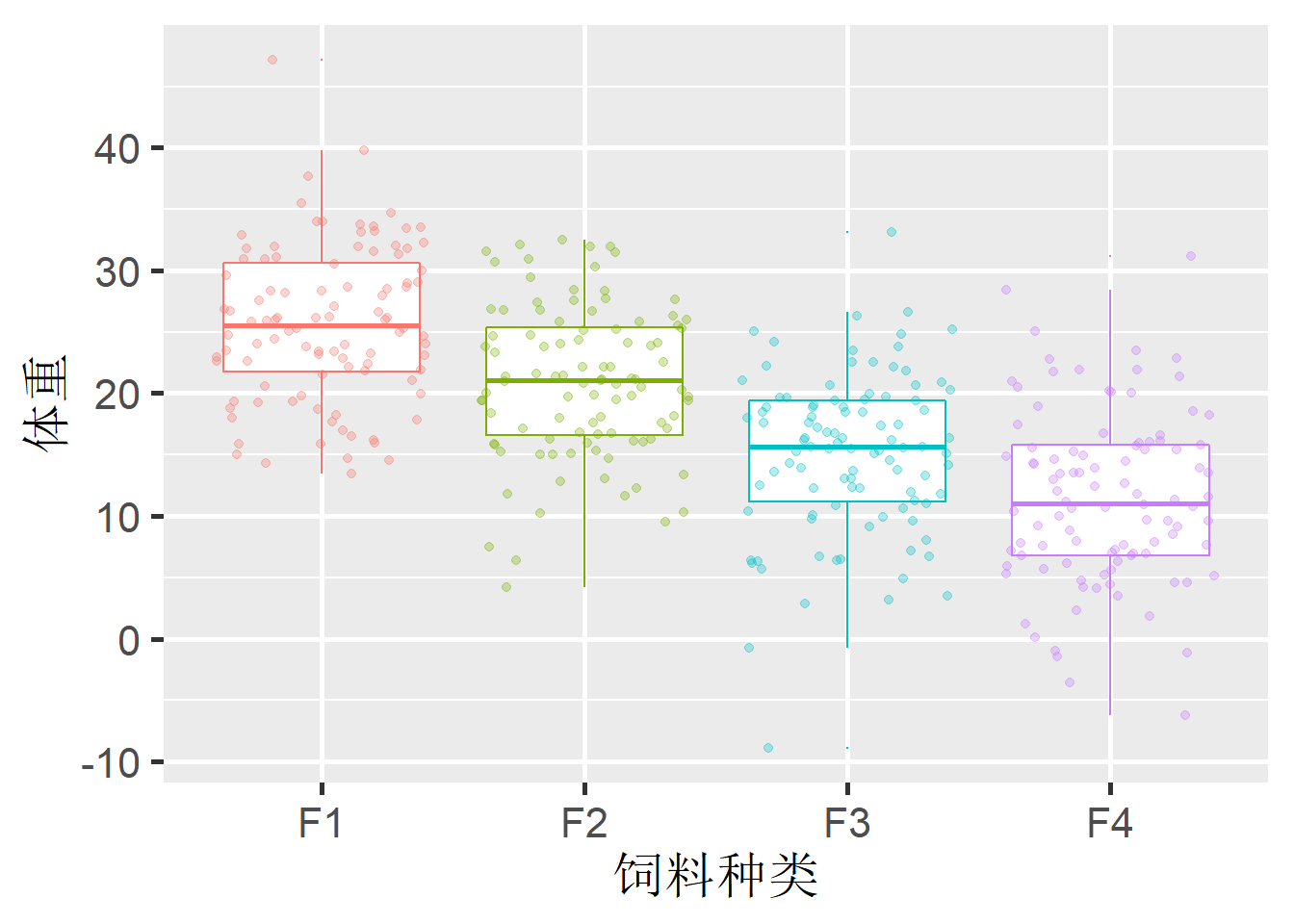
Figure 1: 投喂不同饲料种类后对虾体重分布箱形图
通过上图,从体重均值上可以看出,四种饲料间存在差别。但是,我们需要回答以下几个问题:
- 这种差异有没有偶然因素?从上图中可以看出,每种饲料试验虾的体重都存在较大的变异范围。
- 样本量和实验设计是否满足要求?
- 结果可靠吗?如何对结果的可靠性进行检验?
2.2 方差分析的基本概念
这就需要统计学手段帮我们回答。
首先我们设定一个无效假设:四种饲料投喂对虾后,体重均值相等,没有差异。
\[H_{0}: \mu_{1} = \mu_{2} = \mu_{3} = \mu_{4}\]
然后建立数学模型,检验\(\mu_{i}\)间的差异程度。如果各水平间差异显著,那么就会得出备择假设:
\(H_{1}: \mu_{1}, \mu_{2}, \mu_{3}, \mu_{4}\)不全相等。
我们以单因素方差分析(one-way ANOVA)为例,建立分析不同饲料投喂后体重差异的数学模型:
\[ \left\{\begin{matrix} y_{ij} = \mu + \alpha_{i} + \varepsilon_{ij} \\ \varepsilon_{ij} \sim N(0,\sigma^{2}) \\ \sum_{i=1}^{r}n\alpha_{i} = 0 \end{matrix}\right. \]
上边公式中i=1, 2,…,4,表示饲料种类;\(y_{ij}\)表示投喂第i种饲料后第j尾对虾的体重;\(\mu\)为总体均值;
\(\alpha_{i}\)表示第i种饲料的固定效应,\(\alpha_{i} = \mu_{i} - \mu\),其中\(\mu_{i}\)是第i种饲料的均值;
\(\varepsilon_{ij}\)表示残差,它符合正态分布:均值为0,方差为\(\sigma^{2}\);
要想满足\(\sum_{i=1}^{r}n\alpha_{i} = 0\)这个条件,每个水平下的样本数都应该是一致的。其中r=4,表示四种饲料;n表示每种饲料水平参与测试的样本数。
上述公式表明:如果要对数据进行方差分析,要满足3个基本条件(从线性模型角度看,这三个基本条件非常容易理解):
- 可加性。主要是指处理效应\(\alpha_{i}\)与残差\(\varepsilon_{ij}\)效应是独立的,因此可以加在一起;
- 独立正态性。指的是实验误差\(\varepsilon_{ij}\)应当符合正态分布,而且相互间独立;
- 方差齐性。主要指的是不同处理的方差应该是一致的。也就是说,需要满足假设“\(\sigma^{2}_{1} = \sigma^{2}_{2} = ... = \sigma^{2}_{r}\)。
2.3 总变异的剖分
下边我们进入正题。如何比较处理间的差异?ANOVA的思路是把测量数据的总变异分解为由处理各水平引起的变异和误差变异两部分,然后比较这两部分的大小,通过F检验确定由处理产生的变异是否达到显著水平。
为了检验\(H_{0}\)假设,对平方和、自由度进行分解:
\(S_{T} = \sum_{i=1}^{r}\sum_{j=1}^{n_{i}}(y_{ij}-\bar{y_{\cdot\cdot}})^{2}\),\(\bar{y} = \frac{1}{n}\sum_{i=1}^{r}\sum_{j=1}^{n_{i}}y_{ij}\)
\(S_{T}\)称为总离差平方和,是每个样本数据\(y_{ij}\)与总体均值\(\bar{y_{\cdot\cdot}}\)差的平方和。实际上描绘了总体数据的离散程度。
总离差平方和可以进一步分解为处理平方和、误差平方和:
\[S_{T} = S_{A} + S_{E}\]
其中处理平方和:
\[ S_{A} = \sum_{i=1}^{r}\sum_{j=1}^{n}(y_{i\cdot}-\bar{y_{\cdot\cdot}})^{2} \\ = n\sum_{i=1}^{r}(y_{i\cdot}-\bar{y_{\cdot\cdot}})^{2} \]
误差平方和:
\[S_{E} = \sum_{i=1}^{r}\sum_{j=1}^{n}(y_{ij}-\bar{y_{i\cdot}})^{2}\]
推导过程: \[ S_{T} = \sum_{i=1}^{r}\sum_{j=1}^{n}(y_{ij}-\bar{y_{\cdot\cdot}})^{2} \\ = \sum_{i=1}^{r}\sum_{j=1}^{n}[(y_{ij}-\bar{y_{i\cdot}})+(\bar{y_{i\cdot}}-\bar{y_{\cdot\cdot}})]^{2} \\ = \sum_{i=1}^{r}\sum_{j=1}^{n}(y_{ij}-\bar{y_{i\cdot}})^2+2\sum_{i=1}^{r}\sum_{j=1}^{n}(y_{ij}-\bar{y_{i\cdot}})(\bar{y_{i\cdot}}-\bar{y_{\cdot\cdot}})+\sum_{i=1}^{r}\sum_{j=1}^{n}(\bar{y_{i\cdot}}-\bar{y_{\cdot\cdot}})^{2} \]
由于上边公式中,中间部分为0,因此可以直接推导出:
\[ S_{T} = \sum_{i=1}^{r}\sum_{j=1}^{n}(y_{ij}-\bar{y_{i\cdot}})^2+\sum_{i=1}^{r}\sum_{j=1}^{n}(\bar{y_{i\cdot}}-\bar{y_{\cdot\cdot}})^{2} \\ = S_{E} + S_{A} \]
下边结合第一部分自由度的基础概念,来推导\(S_{T}\)、\(S_{A}\)、\(S_{E}\)的自由度。
对于\(S_{T}\),有rn个样本,根据公式只受总体均值的约束,因此自由度为\(df_{T}=rn-1\);
对于\(S_{A}\),有r个水平,根据公式只受总体均值的约束,因此自由度为\(df_{A}=r-1\);
对于\(S_{E}\),查看它的公式,可以推出,对于处理的每个水平,受各自均值的约束,自由度为n-1,因此r个处理的自由度为\(df_{E} = r(n-1)\)。
计算自由度的目的是什么?有什么用?下边在计算均方时,检验变异的显著性时将会用到。