本部分可能会用到的R包,请提前安装:
- ggplot2 #优秀的作图包
- data.table #优秀的数据转换处理包
- lme4 #提供lmer函数,进行lmm分析
- lmerTest #提供anova函数,对固定效应进行显著性检验
- sjPlot #lmm结果的可视化展示
4.4 包括随机效应的线性混合效应模型
请加载一个新的数据集shrimpex.csv,其中有一个PopID字段,包括Pop1到Pop4共计4个水平,表示shrimp数据由四个群体组成。现在考虑这样一个问题:四个群体间收获体重是否存在差异。
首先加载数据文件。画出四个群体收获体重的箱形图,加上jitter点。
注意,下边代码,shrimpex.csv文件保存在了datasets文件夹下。该文件夹与x需与R脚本文件在同一目录下。
shrimp <- fread(input = "datasets/shrimpex.csv",sep = ",",header = TRUE,stringsAsFactors = TRUE)
str(shrimp)## Classes 'data.table' and 'data.frame': 4282 obs. of 10 variables:
## $ AnimalID: Factor w/ 4282 levels "13G1000001","13G1000002",..: 3308 3307 2215 1303 3601 2184 2194 2175 1585 2176 ...
## $ SireID : Factor w/ 100 levels "12G000K010","12G000K065",..: 81 81 81 81 81 81 81 81 81 81 ...
## $ DamID : Factor w/ 91 levels "12G000K052","12G000K097",..: 81 81 81 81 81 81 81 81 81 81 ...
## $ PopID : Factor w/ 4 levels "Pop1","Pop2",..: 1 1 1 1 1 1 1 1 1 1 ...
## $ FamilyID: Factor w/ 105 levels "13F1306003","13F1306004",..: 6 6 6 6 6 6 6 6 6 6 ...
## $ SexID : Factor w/ 2 levels "Female","Male": 2 2 1 1 1 2 1 2 2 1 ...
## $ TankID : Factor w/ 2 levels "T1","T2": 1 1 1 1 1 1 1 1 1 1 ...
## $ M1BW : num 8.13 8.13 8.13 8.13 8.13 8.55 8.55 8.55 8.55 8.55 ...
## $ M2BW : num 29 30.5 33.3 40.1 43 29.1 30.7 30.7 32.5 35.6 ...
## $ M2Age : int 219 219 219 219 219 219 219 219 219 219 ...
## - attr(*, ".internal.selfref")=<externalptr>ggplot(data=shrimp,aes(x=PopID,y=M2BW,color=PopID)) +
geom_boxplot(outlier.size = 0)+
geom_jitter(alpha=0.3)+
labs(x="群体",y="收获体重")+
theme_gray(base_size = 20)+
theme(legend.position = "none")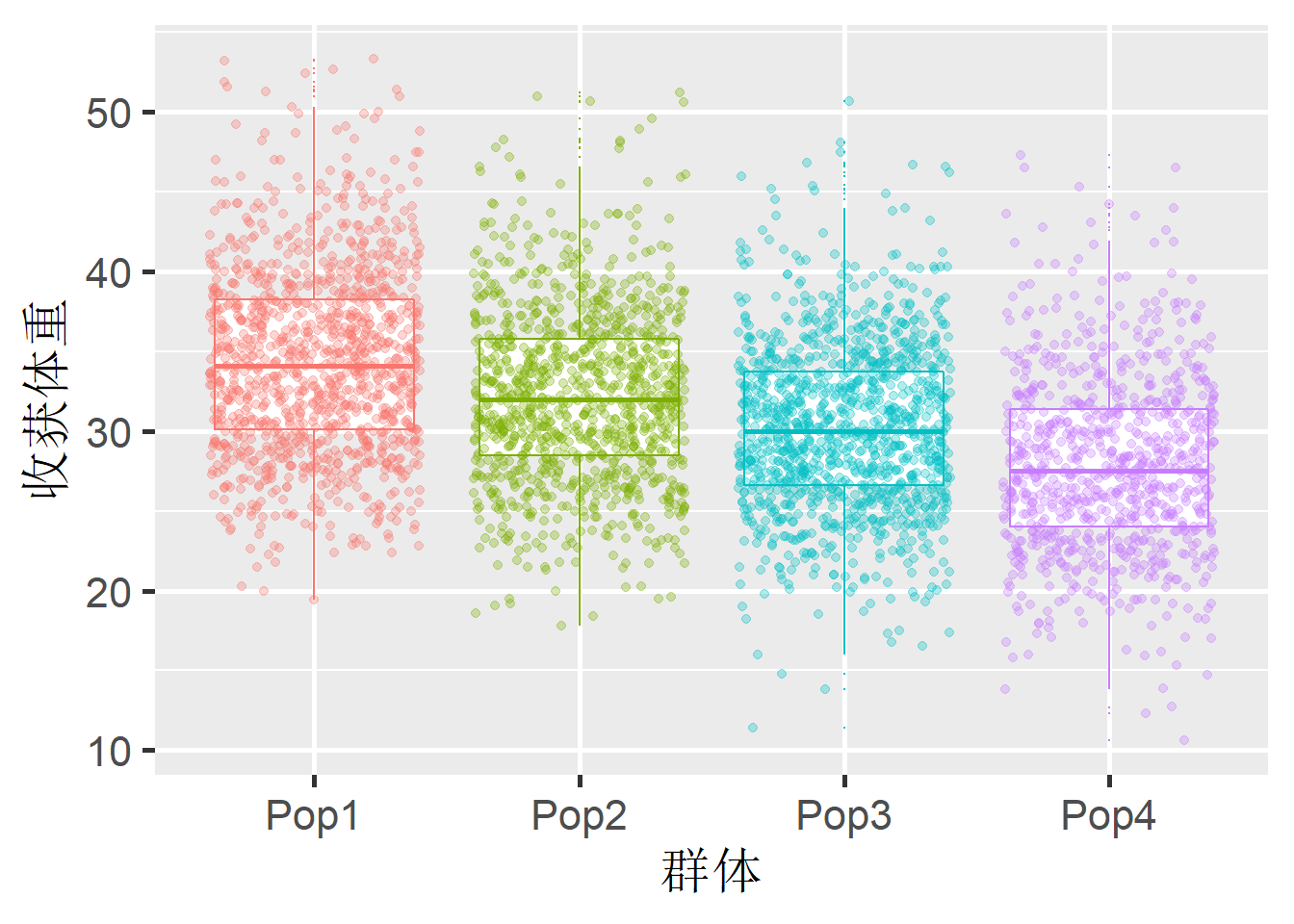
Figure 1: 四个对虾群体收获体重的箱形图
从上图中,大致可以看出,群体间是存在差异的。
进一步分析数据,你会发现每个群体由多个家系组成,见下图。
ggplot(data=shrimp,aes(x=PopID,y=M2BW,fill=FamilyID)) +
geom_boxplot(outlier.size = 0)+
labs(x="群体",y="收获体重")+
theme_gray(base_size = 20)+
theme(legend.position = "none")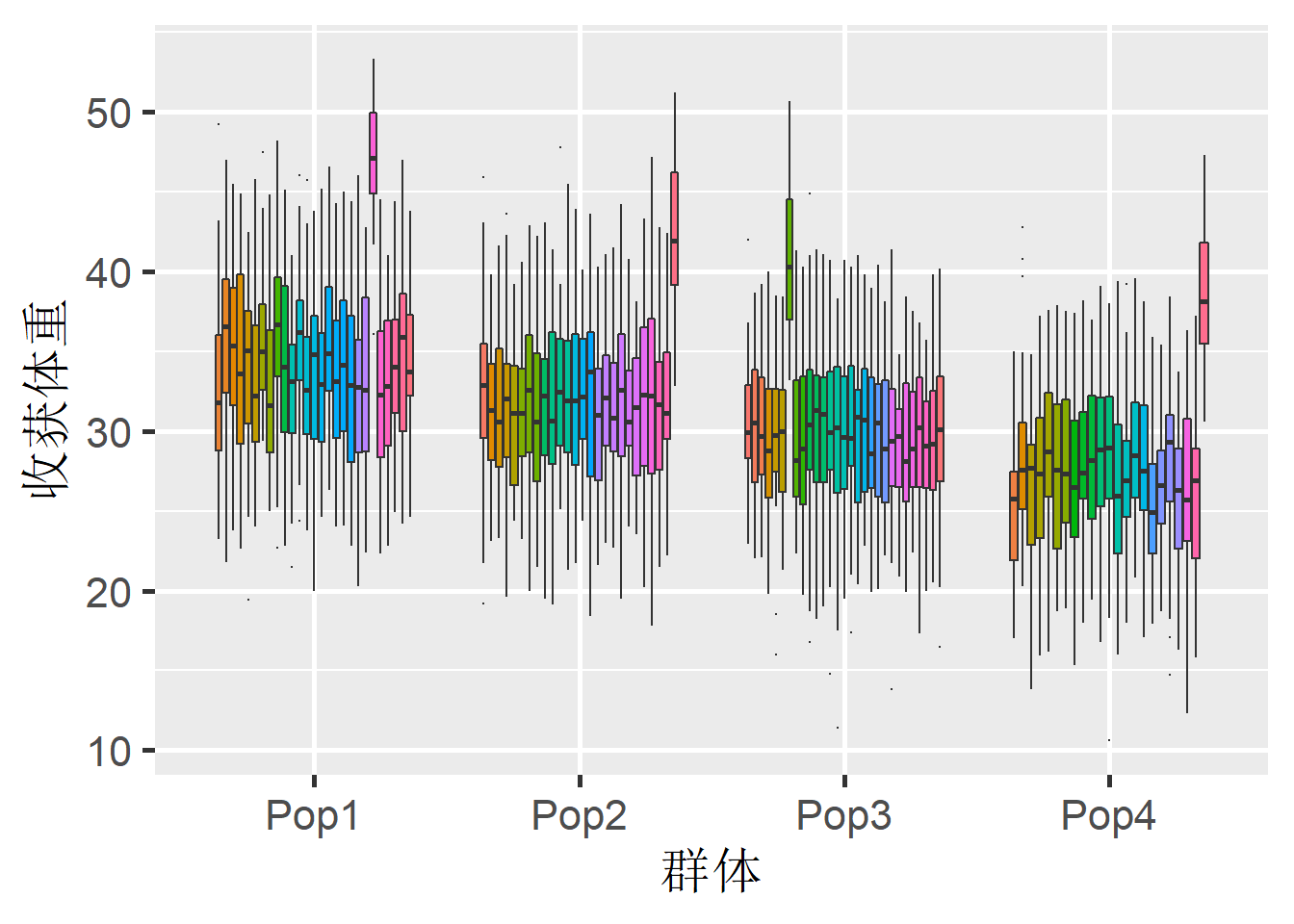
Figure 2: 四个对虾群体内家系收获体重的箱形图
这里遇到了一个问题,在评价群体间的差异时,是否需要考虑每个群体内的家系结构?
理论上,我们从每个群体抽样时,抽样个体是代表该群体的随机样本。但是,一个群体内的个体往往存在亲缘关系,譬如(全同胞、半同胞个体)。因此抽样个体存在两个层次:每个群体包括多个家系,每个家系包括数量不等的个体。
从上图中可以看出,每个群体内的不同家系间是存在差异的。
每一个家系内的个体,遗传自同一对亲本,相互间相似性更强。不同家系个体的体重均值是不一样的。
这实际上违背了样本观察值的独立性原则,同一个家系内的全同胞个体的体重值实际上是由他们亲本所决定。
针对这种情况,我们把家系效应作为随机效应加入模型中。这相当于,给每个家系设置一个基线,类似于不同的家系有不同的平均体重,也称作随机截距(random intercept)。
在模型中加入家系随机效应,那么观察值的非独立性问题就解决了。
为了说明家系结构对分析结果的影响,故意在每个群体中设置了一个均值特别高的家系。在实际测试数据中,这种现象也会经常出现。如果我们分析时不考虑群体内的家系结构,那么家系方差会被累加到残差方差中。
如果采取方差分析的方法,你也会发现,忽略家系结构,群体的均方值可能会非常大,被严重高估。
根据教程1对于固定效应和随机效应的讨论,由于我们的目的是要分析四个群体间的差异,获得每个群体的性能,因此群体更适合做固定效应。每个群体是由多个家系组成的,这些家系只是大量家系的一个随机抽样,因此更加适合作为随机效应。
下边我们通过两个模型实例,来看一下家系结构对分析结果的影响。
\[M2BW = Pop + Sex + Tank + Sex:M1BW\]
模型8不考虑家系结构,Pop、Sex和Tank为固定效应,Sex:M1BW为协变量。
分析结果如下:
shrimp.lm.8 <- lm(M2BW ~ 1 + PopID + SexID + TankID + SexID:M1BW,shrimp)
summary(shrimp.lm.8) #加载lmerTest包后,lmer的返回结果,每个固定效应系数带有P值##
## Call:
## lm(formula = M2BW ~ 1 + PopID + SexID + TankID + SexID:M1BW,
## data = shrimp)
##
## Residuals:
## Min 1Q Median 3Q Max
## -20.7242 -2.5787 -0.2092 2.2353 18.9070
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 35.42932 0.53924 65.702 < 2e-16 ***
## PopIDPop2 -1.61211 0.18406 -8.759 < 2e-16 ***
## PopIDPop3 -3.61817 0.18086 -20.005 < 2e-16 ***
## PopIDPop4 -5.76930 0.21237 -27.166 < 2e-16 ***
## SexIDMale -5.39346 0.70557 -7.644 2.59e-14 ***
## TankIDT2 -2.93073 0.13206 -22.192 < 2e-16 ***
## SexIDFemale:M1BW 0.40396 0.06778 5.960 2.73e-09 ***
## SexIDMale:M1BW 0.30223 0.07363 4.105 4.13e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 4.296 on 4233 degrees of freedom
## (41 observations deleted due to missingness)
## Multiple R-squared: 0.4845, Adjusted R-squared: 0.4837
## F-statistic: 568.4 on 7 and 4233 DF, p-value: < 2.2e-16anova(shrimp.lm.8) #lmerTest包提供该函数## Analysis of Variance Table
##
## Response: M2BW
## Df Sum Sq Mean Sq F value Pr(>F)
## PopID 3 23856 7952 430.856 < 2.2e-16 ***
## SexID 1 39588 39588 2144.973 < 2.2e-16 ***
## TankID 1 9106 9106 493.407 < 2.2e-16 ***
## SexID:M1BW 2 889 445 24.095 3.934e-11 ***
## Residuals 4233 78124 18
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1模型9考虑家系结构,Pop:Family为随机效应,Pop、Sex和Tank为固定效应,Sex:M1BW为协变量。
\[M2BW = Pop + Sex + Tank + Sex:M1BW + Pop:Family\]
在模型中加入随机效应,需要使用lme4包中的lmer函数。下边代码中的(1|PopID:FamilyID),表示针对不同的家系,单独估计其随机截距(random intercept)。其中1表示随机截距。
分析结果如下:
shrimp.lm.9 <- lmer(M2BW ~ 1 + PopID + SexID + TankID + SexID:M1BW + (1|PopID:FamilyID),shrimp)
summary(shrimp.lm.9)## Linear mixed model fit by REML. t-tests use Satterthwaite's method [
## lmerModLmerTest]
## Formula:
## M2BW ~ 1 + PopID + SexID + TankID + SexID:M1BW + (1 | PopID:FamilyID)
## Data: shrimp
##
## REML criterion at convergence: 23070.4
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -5.5304 -0.5854 0.0240 0.6388 3.8977
##
## Random effects:
## Groups Name Variance Std.Dev.
## PopID:FamilyID (Intercept) 5.933 2.436
## Residual 12.527 3.539
## Number of obs: 4241, groups: PopID:FamilyID, 105
##
## Fixed effects:
## Estimate Std. Error df t value Pr(>|t|)
## (Intercept) 35.7188 1.0605 487.3240 33.683 < 2e-16 ***
## PopIDPop2 -1.6596 0.6884 100.5550 -2.411 0.01774 *
## PopIDPop3 -3.7742 0.6733 101.7519 -5.606 1.78e-07 ***
## PopIDPop4 -5.8638 0.7359 110.5088 -7.968 1.58e-12 ***
## SexIDMale -5.6599 0.5901 4148.3019 -9.591 < 2e-16 ***
## TankIDT2 -2.9491 0.1097 4140.0606 -26.884 < 2e-16 ***
## SexIDFemale:M1BW 0.3757 0.1204 992.9529 3.122 0.00185 **
## SexIDMale:M1BW 0.2904 0.1231 1068.2960 2.360 0.01847 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Correlation of Fixed Effects:
## (Intr) PpIDP2 PpIDP3 PpIDP4 SxIDMl TnIDT2 SIDF:M
## PopIDPop2 -0.384
## PopIDPop3 -0.419 0.506
## PopIDPop4 -0.519 0.476 0.494
## SexIDMale -0.248 0.002 0.007 -0.004
## TankIDT2 -0.042 -0.006 -0.004 -0.001 -0.030
## SxIDFm:M1BW -0.889 0.077 0.108 0.250 0.291 -0.010
## SxIDMl:M1BW -0.711 0.074 0.100 0.246 -0.352 0.010 0.786anova(shrimp.lm.9)## Type III Analysis of Variance Table with Satterthwaite's method
## Sum Sq Mean Sq NumDF DenDF F value Pr(>F)
## PopID 914.2 304.7 3 103.8 24.3255 5.319e-12 ***
## SexID 1152.4 1152.4 1 4148.3 91.9951 < 2.2e-16 ***
## TankID 9053.7 9053.7 1 4140.1 722.7464 < 2.2e-16 ***
## SexID:M1BW 122.4 61.2 2 1414.2 4.8839 0.007695 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1把模型8的Residual standard error的平方,与模型9 Random Effects部分对比,你会发现,如果不考虑家系结构,残差方差明显被高估,估计值为18.4559804 。考虑家系结构后,残差方差为12.5267429, 明显变小, 从残差中分离出了大部分的家系方差。由家系随机效应产生的方差,估计值为5.9328232,占表型方差的32%。
从anova方差分析(如果对基础概念不了解,可参考这篇blog:自由度和方差分析)的角度看,加入家系随机效应后,群体固定效应(PopID)尽管仍然也达到了显著水平,但是均方和F值明显变小。这表明存在这样一种风险,如果考虑群体内的家系结构,本来两个群体的差异可能达不到显著水平,但是如果忽视了这种家系结构,两个群体间的差异统计上会表现为显著水平,从而误判群体间的实际性能差别。
我们看一下,基于模型9(不包括家系的随机效应),预测四个群体家系的性能,如下图所示:你会发现,每个群体中特别大的家系效应,已经被剔除掉了。
ps:拟合值反应的是包括所有固定和随机效应的结果,lmer中通过fitted()函数获得该值。预测值,是可以设定不包括随机效应的,lmer中通过predict()函数获得该值。
shrimp.lm.9.predict <- predict(shrimp.lm.9,re.form=NA) #拟合值
shrimp.lm.9.predict.dt <- data.table(ObsSeq =as.integer(names(shrimp.lm.9.predict)),PredictedValue=shrimp.lm.9.predict)
shrimp[,":="(ObsSeq=seq(nrow(shrimp)))]
#把拟合值合并到shrimp数据集
shrimp.predicted.value <- merge(shrimp,shrimp.lm.9.predict.dt,by = c("ObsSeq"),all.y = TRUE)
ggplot(data=shrimp.predicted.value,aes(x=PopID,y=PredictedValue,fill=FamilyID)) +
geom_boxplot(outlier.size = 0)+
labs(x="群体",y="收获体重预测值")+
theme_gray(base_size = 20)+
theme(legend.position = "none")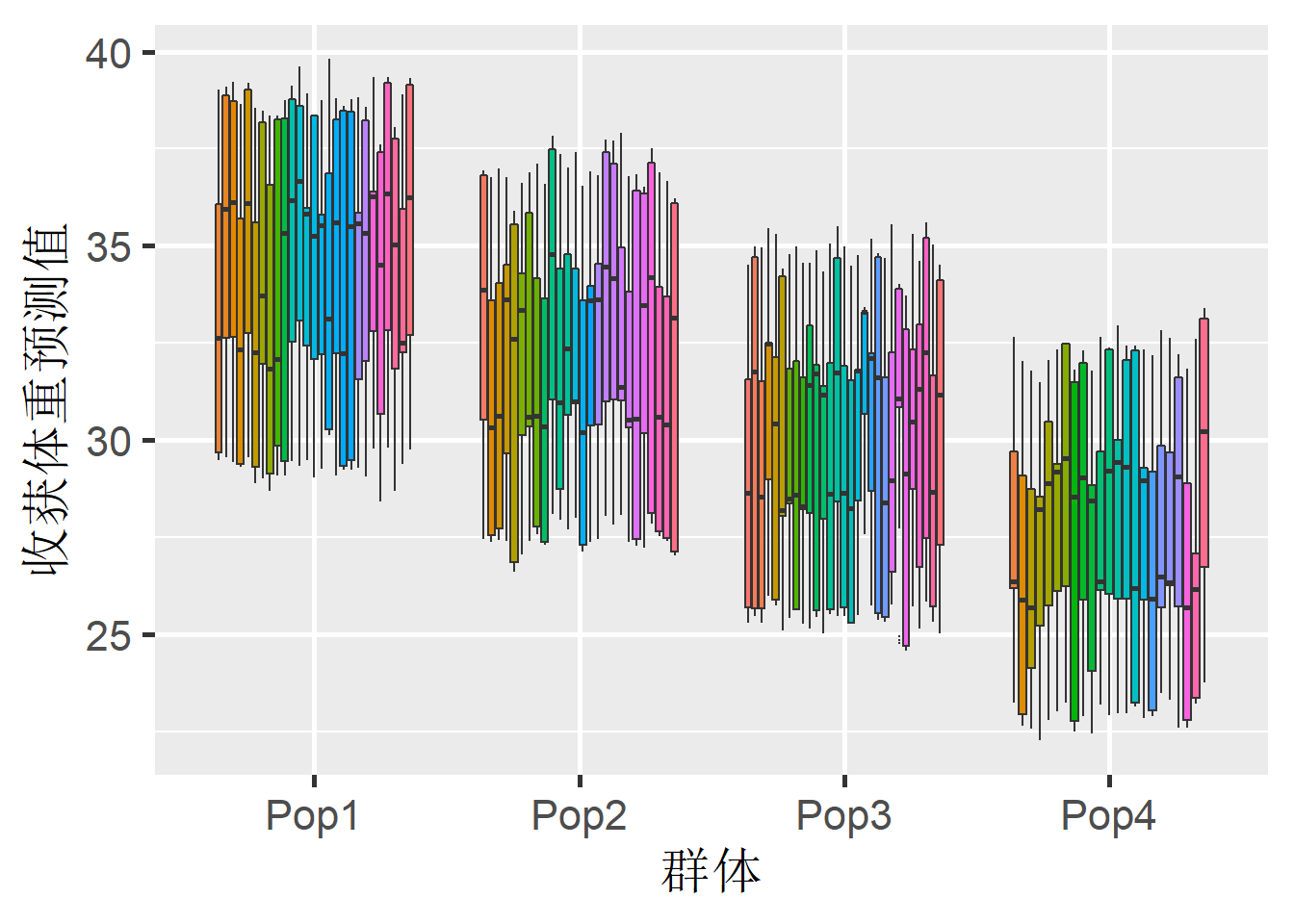
Figure 3: 四个对虾群体体重的预测值
4.5 随机效应的显著性检验
模型中加入随机效应后,如何检验其显著性?
一般是通过似然比率检验(Likelihood ratio test, LRT)来实现。lmerTest包中的rand()函数提供该功能。
首先我们来看一下似然比率检验的结果:
rand(shrimp.lm.9)## ANOVA-like table for random-effects: Single term deletions
##
## Model:
## M2BW ~ PopID + SexID + TankID + (1 | PopID:FamilyID) + SexID:M1BW
## npar logLik AIC LRT Df Pr(>Chisq)
## <none> 10 -11535 23090
## (1 | PopID:FamilyID) 9 -12206 24430 1341.4 1 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1卡方检验表明,p<0.01,模型中加入PopID:Family随机效应后,对样本数据拟合得更好。
LRT检验的公式为\(LR = 2*(lnL1 - lnL2)\),其中L1为复杂模型的最大似然值,L2为简单模型的最大似然值。对L1和L2分别取log转换,计算LR值。然后通过卡方检验,确定p值。自由度为复杂模型和简单模型包括的随机效应数之差。
模型9的最大似然值log转换后为:\(-1.153518\times 10^{4}\);
不包括PopID:Family随机效应的模型8的logLikelihood值为\(-1.21958\times 10^{4}\)。
lmer函数返回的最大似然值log转换通过lme4包的logLik()函数实现。对于lm函数返回的最大似然值,stats包也有对应的logLik()函数处理。
似然比率为:LR = 2*(-11535.178901292 - -12195.7957678913) = 1321.23。自由度为1。
跟直接利用rand()函数获得的卡方值相比略有出入。
4.5 获得每个群体的性能
调用emmeans包中的函数,计算四个群体的估计边际均值(estimated marginal means),或者说最小二乘均值(least-squares means)。根据边际均值,我们可以对群体的性能进行排序和比较。
关于emmeans包,请参考日志最小二乘均值的估计模型。尽管该日志介绍的是lsmeans包,但用法跟emmeans包都是一样的。而且根据作者介绍,在不久的将来,emmeans包要替代lsmeans包。
注意,安装emmeans还需要pbkrtest包,这个包没有自动安装,需要手动安装。
require(emmeans)## Loading required package: emmeansshrimp.lm9.rgl <- ref_grid(shrimp.lm.9)## Note: D.f. calculations have been disabled because the number of observations exceeds 3000.
## To enable adjustments, set emm_options(pbkrtest.limit = 4241) or larger,
## but be warned that this may result in large computation time and memory use.## Note: D.f. calculations have been disabled because the number of observations exceeds 3000.
## To enable adjustments, set emm_options(lmerTest.limit = 4241) or larger,
## but be warned that this may result in large computation time and memory use.emmeans(shrimp.lm9.rgl,"PopID")## PopID emmean SE df asymp.LCL asymp.UCL
## Pop1 33.8 0.485 Inf 32.9 34.8
## Pop2 32.2 0.490 Inf 31.2 33.1
## Pop3 30.1 0.466 Inf 29.2 31.0
## Pop4 28.0 0.537 Inf 26.9 29.0
##
## Results are averaged over the levels of: SexID, TankID
## Degrees-of-freedom method: asymptotic
## Confidence level used: 0.95从上边结果中查找emmean列,可以看到Pop1群体的边际均值最大,这表明四个群体中该群体性能最好。